《2025年一遍过八年级数学上册北师大版》

1 [2024沈阳期末]目前,全球淡水资源日益减少,提倡全社会节约用水已成为全球的共识。据测试:拧不紧的水龙头每分钟滴出60滴水,每滴水约0.05毫升。小康洗手后,没有把水龙头拧紧,水龙头按测试的速度滴水。设小康离开x分钟后,水龙头滴出y毫升的水,则y与x之间的关系式是 (B)
A. $ y = 0.05x $
B. $ y = 3x $
C. $ y = 60x $
D. $ y = 0.05x + 60 $

答案： B 由题意，得 $ y = 60 \times 0.05x = 3x $。

2 [2025大庆十六中期中]已知蓄水池有水$50m^3,$现匀速放水,池中水量和放水时间的关系如表所示,则放水14min时,池中水量为 (A)

$A. 22m^3 B. 24m^3 C. 26m^3 D. 28m^3$

答案： A 由题意知，蓄水池中水量每分钟减少 $ 2 \, \text{m}^3 $，设池中水量为 $ y \, \text{m}^3 $，放水时间为 $ t \, \text{min} $，所以 $ y = 50 - 2t $，所以当 $ t = 14 $ 时，$ y = 22 $，即当放水 $ 14 \, \text{min} $ 时，水池中有水 $ 22 \, \text{m}^3 $。

3 [2025西安雁塔区模拟]一蜡烛高20厘米,点燃后平均每小时燃掉4厘米,则蜡烛点燃后剩余的高度h(厘米)与燃烧时间t(时)之间的关系式是$ h = $$ 20 - 4t $$ (0 \leq t \leq 5) $。

答案： $ 20 - 4t $ 因为蜡烛高 $ 20 $ 厘米，蜡烛点燃后平均每小时燃掉 $ 4 $ 厘米，所以 $ h = 20 - 4t $。

在某次综合与实践活动中,小华同学了解到鞋号(码)与脚长(毫米)的对应关系如表所示:

若小华的脚长为259毫米,则他的鞋号是42码。

答案： $ 42 $ 因为 $ 215 = 33 \times 5 + 50 $，$ 220 = 34 \times 5 + 50 $，$ 225 = 35 \times 5 + 50 $，$ 230 = 36 \times 5 + 50 $，$ 235 = 37 \times 5 + 50 $，…，所以脚长 $ = $ 鞋码 $ \times 5 + 50 $，若设脚长为 $ y $ 毫米，鞋号为 $ x $ 码，则 $ y = 5x + 50 $，将 $ y = 259 $ 代入 $ y = 5x + 50 $，得 $ 259 = 5x + 50 $，解得 $ x = 41.8 $，所以他的鞋号是 $ 42 $ 码。

5 [2025潍坊期中]数学兴趣小组通过查阅资料发现,声音在空气中传播的速度和气温的变化存在如下的关系:
阅读上述材料,回答下列问题:

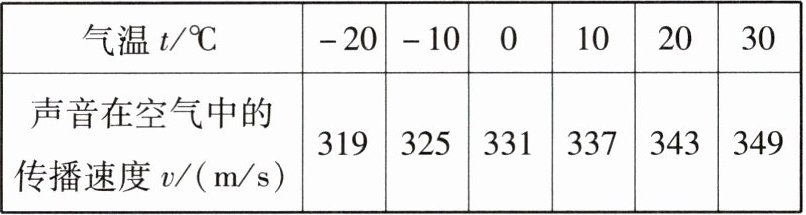
(1)从表中数据可知,气温每升高1℃,声音在空气中传播的速度提高了0.6m/s?
(2)用含t的代数式表示v。v=331+0.6t
(3)某日的气温为15℃,小莹同学看到烟花燃放后5s才听到声响,那么小莹同学与燃放烟花所在地大约相距1700m?

答案： 解：
(1) 从表中数据可知，气温每升高 $ 10 \, ^ { \circ } \text{C} $，声音在空气中传播的速度提高了 $ 6 \, \text{m/s} $，所以气温每升高 $ 1 \, ^ { \circ } \text{C} $，声音在空气中传播的速度提高了 $ 0.6 \, \text{m/s} $。
(2) 因为气温每升高 $ 1 \, ^ { \circ } \text{C} $，声音在空气中传播的速度提高了 $ 0.6 \, \text{m/s} $，且当 $ t = 0 $ 时，$ v = 331 $，所以 $ v = 331 + 0.6t $。
(3) 当 $ t = 15 $ 时，$ v = 331 + 0.6 \times 15 = 340 $，$ 340 \times 5 = 1700 $，所以小莹同学与燃放烟花所在地大约相距 $ 1700 \, \text{m} $。

6 [2024西安爱知中学期末]在学习地理时,我们知道“海拔越高,气温越低”。下表是海拔h(km)与此高度处气温t(℃)的关系。根据下表,回答以下问题:

(1)由表可知,距离地面高度每上升1km,温度降低______℃。
(2)写出气温t与海拔h的关系式;并求出当海拔高度是7km时,气温是多少?
(3)某航班飞机在执行飞行任务至一定高度时,驾驶舱突现险情,此时舱外气温为-38.2℃。两名飞行员冷静应对,创造了世界航空史上的奇迹,请你计算出该飞机发生险情时的海拔(假设当时所在位置的地面温度为20℃)。
(1)由表可知,距离地面高度每上升1km,温度降低6℃。
(2)写出气温t与海拔h的关系式;并求出当海拔高度是7km时,气温是多少?
气温t与海拔h的关系式为t=20-6h，当海拔高度是7km时,气温是-22℃。
(3)某航班飞机在执行飞行任务至一定高度时,驾驶舱突现险情,此时舱外气温为-38.2℃。两名飞行员冷静应对,创造了世界航空史上的奇迹,请你计算出该飞机发生险情时的海拔(假设当时所在位置的地面温度为20℃)。
该飞机发生险情时的海拔为9.7km。

答案： 解：
(1) $ 6 $ 距离地面高度每上升 $ 1 \, \text{km} $，温度降低 $ 20 - 14 = 6 ( ^ { \circ } \text{C} ) $。
(2) 气温 $ t $ 与海拔 $ h $ 的关系式为 $ t = 20 - 6h $，当 $ h = 7 $ 时，$ t = 20 - 6 \times 7 = - 22 $，所以气温 $ t $ 与海拔 $ h $ 的关系式为 $ t = 20 - 6h $，当海拔是 $ 7 \, \text{km} $ 时，气温是 $ - 22 \, ^ { \circ } \text{C} $。
(3) 当 $ t = - 38.2 $ 时，$ 20 - 6h = - 38.2 $，解得 $ h = 9.7 $，所以该飞机发生险情时的海拔高度为 $ 9.7 \, \text{km} $。