第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1 [2024益阳大通湖区模拟]我市某九年一贯制学校共有学生3000人,计划一年后初中在校生增加8%,小学在校生增加11%,这样全校在校生将增加10%,设这所学校现初中在校生x人,小学在校生y人,由题意可列方程组为(
A. $\left\{\begin{array}{l}x+y= 3000,\\ 8\%x+11\%y= 3000× 10\%\end{array}\right.$
B. $\left\{\begin{array}{l}x+y= 3000,\\ 8\%x+11\%y= 3000× (1+10\%)\end{array}\right.$
C. $\left\{\begin{array}{l}x+y= 3000,\\ (1+8\%)x+(1+11\%)y= 3000× 10\%\end{array}\right.$
D. $\left\{\begin{array}{l}x+y= 3000,\\ 8\%x+11\%y= 10\%\end{array}\right.$
$\left\{\begin{array}{l} x + y = 3000,\\ 8\%x + 11\%y = 3000×10\%\end{array}\right.$或$\left\{\begin{array}{l} x + y = 3000,\\ (1 + 8\%)x + (1 + 11\%)y = 3000×(1 + 10\%)\end{array}\right.$
)A. $\left\{\begin{array}{l}x+y= 3000,\\ 8\%x+11\%y= 3000× 10\%\end{array}\right.$
B. $\left\{\begin{array}{l}x+y= 3000,\\ 8\%x+11\%y= 3000× (1+10\%)\end{array}\right.$
C. $\left\{\begin{array}{l}x+y= 3000,\\ (1+8\%)x+(1+11\%)y= 3000× 10\%\end{array}\right.$
D. $\left\{\begin{array}{l}x+y= 3000,\\ 8\%x+11\%y= 10\%\end{array}\right.$
答案:
A 因为这所学校现初中在校生x人,小学在校生y人,计划一年后初中在校生增加8%,小学在校生增加11%,所以一年后初中在校生有$(1 + 8\%)x$人,增加了$8\%x$人,小学在校生有$(1 + 11\%)y$人,增加了$11\%y$人。因为全校在校生将增加10%,所以一年后全校在校生有$3000×(1 + 10\%)$人,增加了$3000×10\%$人。所以可列方程组为$\left\{\begin{array}{l} x + y = 3000,\\ 8\%x + 11\%y = 3000×10\%\end{array}\right.$或$\left\{\begin{array}{l} x + y = 3000,\\ (1 + 8\%)x + (1 + 11\%)y = 3000×(1 + 10\%)\end{array}\right.$。
2 [2025沈阳皇姑区期末]小明家种植水果,去年收支相抵后,结余1200元,今年因为改进了种植技术,他家水果获得丰收,收入比去年增加15%,支出比去年减少5%,今年比去年多结余1140元,则小明家去年收入
6000
元,支出4800
元。
答案:
6000 4800 设小明家去年收入x元,支出y元,由题意,得$\left\{\begin{array}{l} x - y = 1200,\\ (1 + 15\%)x - (1 - 5\%)y = 1200 + 1140,\end{array}\right.$解得$\left\{\begin{array}{l} x = 6000,\\ y = 4800,\end{array}\right.$即小明家去年收入6000元,支出4800元。
3 今年“五一”小长假期间,某市外来与外出旅游的总人数为287万人,分别比去年同期增长35%和25%,去年同期外来旅游的人数比外出旅游的人数多20万人。求该市今年外来和外出旅游的人数。
答案:
解:设去年同期外来旅游的人数为x万人,外出旅游的人数为y万人,
依题意,得$\left\{\begin{array}{l} x - y = 20,\\ (1 + 35\%)x + (1 + 25\%)y = 287,\end{array}\right.$
解得$\left\{\begin{array}{l} x = 120,\\ y = 100,\end{array}\right.$
所以$(1 + 35\%)x = (1 + 35\%)×120 = 162,(1 + 25\%)y = (1 + 25\%)×100 = 125$。
答:该市今年外来旅游的人数为162万人,外出旅游的人数为125万人。
依题意,得$\left\{\begin{array}{l} x - y = 20,\\ (1 + 35\%)x + (1 + 25\%)y = 287,\end{array}\right.$
解得$\left\{\begin{array}{l} x = 120,\\ y = 100,\end{array}\right.$
所以$(1 + 35\%)x = (1 + 35\%)×120 = 162,(1 + 25\%)y = (1 + 25\%)×100 = 125$。
答:该市今年外来旅游的人数为162万人,外出旅游的人数为125万人。
4 [2024渭南临渭区期末]某配餐公司需用甲、乙两种食材为在校午餐的同学配置营养餐,两种食材每克所含的蛋白质含量和碳水化合物含量如下表所示:

若每位中学生每餐需要21单位蛋白质和40单位碳水化合物,那么每餐甲、乙两种食材各多少克恰好满足一个中学生的需要?设每餐需要甲食材x克,乙食材y克,那么可列方程组为

若每位中学生每餐需要21单位蛋白质和40单位碳水化合物,那么每餐甲、乙两种食材各多少克恰好满足一个中学生的需要?设每餐需要甲食材x克,乙食材y克,那么可列方程组为
$\left\{\begin{array}{l} 0.3x + 0.7y = 21,\\ 0.6x + 0.4y = 40\end{array}\right.$
。
答案:
$\left\{\begin{array}{l} 0.3x + 0.7y = 21,\\ 0.6x + 0.4y = 40\end{array}\right.$
5 [2024华东师大附属杭州学校期中]甲、乙两人从相距18km的两地同时出发,相向而行,经$\frac{9}{5}$h相遇。如果甲比乙先出发$\frac{2}{3}$h,那么在乙出发后经$\frac{3}{2}$h两人相遇。则甲的速度为
$\frac{9}{2}$
km/h。
答案:
$\frac{9}{2}$ 解题思路:设甲的速度为x km/h,乙的速度为y km/h,借助表格分析如下:
|两种情况|甲的路程|乙的路程|甲、乙两人路程之和|
|----|----|----|----|
|第一种情况(同时出发)|$\frac{9}{5}x$|$\frac{9}{5}y$|$\frac{9}{5}x + \frac{9}{5}y$|
|第二种情况(甲比乙先出发)|$(\frac{2}{3} + \frac{3}{2})x$|$\frac{3}{2}y$|$(\frac{2}{3} + \frac{3}{2})x + \frac{3}{2}y$|
设甲的速度为x km/h,乙的速度为y km/h,由题意,得$\left\{\begin{array}{l} \frac{9}{5}x + \frac{9}{5}y = 18,\\ (\frac{2}{3} + \frac{3}{2})x + \frac{3}{2}y = 18,\end{array}\right.$解得$\left\{\begin{array}{l} x = \frac{9}{2},\\ y = \frac{11}{2},\end{array}\right.$即甲的速度为$\frac{9}{2}$km/h,乙的速度为$\frac{11}{2}$km/h。
|两种情况|甲的路程|乙的路程|甲、乙两人路程之和|
|----|----|----|----|
|第一种情况(同时出发)|$\frac{9}{5}x$|$\frac{9}{5}y$|$\frac{9}{5}x + \frac{9}{5}y$|
|第二种情况(甲比乙先出发)|$(\frac{2}{3} + \frac{3}{2})x$|$\frac{3}{2}y$|$(\frac{2}{3} + \frac{3}{2})x + \frac{3}{2}y$|
设甲的速度为x km/h,乙的速度为y km/h,由题意,得$\left\{\begin{array}{l} \frac{9}{5}x + \frac{9}{5}y = 18,\\ (\frac{2}{3} + \frac{3}{2})x + \frac{3}{2}y = 18,\end{array}\right.$解得$\left\{\begin{array}{l} x = \frac{9}{2},\\ y = \frac{11}{2},\end{array}\right.$即甲的速度为$\frac{9}{2}$km/h,乙的速度为$\frac{11}{2}$km/h。
6 [2024安徽中考]乡村振兴战略实施以来,很多外出人员返乡创业。某村有部分返乡青年承包了一些田地,采用新技术种植A,B两种农作物。种植这两种农作物每公顷所需人数和投入资金如下表:
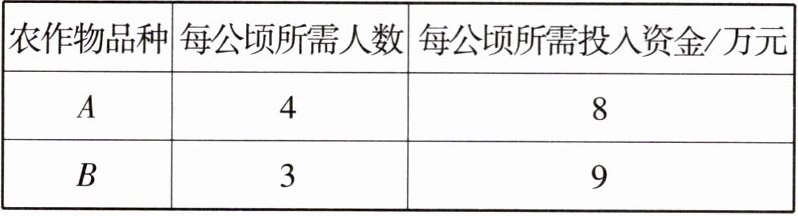
已知农作物种植人员共24位,且每人只参与一种农作物种植,投入资金共60万元,问A,B这两种农作物的种植面积各多少公顷。
A种农作物的种植面积是

已知农作物种植人员共24位,且每人只参与一种农作物种植,投入资金共60万元,问A,B这两种农作物的种植面积各多少公顷。
A种农作物的种植面积是
3
公顷,B种农作物的种植面积是4
公顷。
答案:
解:设A种农作物的种植面积是x公顷,B种农作物的种植面积是y公顷,
根据题意,得$\left\{\begin{array}{l} 4x + 3y = 24,\\ 8x + 9y = 60,\end{array}\right.$解得$\left\{\begin{array}{l} x = 3,\\ y = 4,\end{array}\right.$
所以A种农作物的种植面积是3公顷,B种农作物的种植面积是4公顷。
根据题意,得$\left\{\begin{array}{l} 4x + 3y = 24,\\ 8x + 9y = 60,\end{array}\right.$解得$\left\{\begin{array}{l} x = 3,\\ y = 4,\end{array}\right.$
所以A种农作物的种植面积是3公顷,B种农作物的种植面积是4公顷。
查看更多完整答案,请扫码查看


