《2025年一遍过八年级数学上册北师大版》

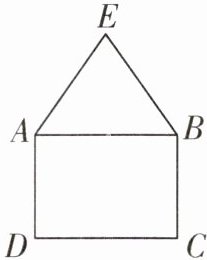
1 新趋势·结论开放 教材例题变式 如图,在长方形ABCD中,已知AB= 6,AD= 4,在长方形ABCD外画△ABE,使AE= BE= 5,请建立适当的平面直角坐标系,并写出各顶点的坐标。

答案：
解:答案不唯一。如图,以边AB所在直线为x轴,以边AB的中垂线为y轴建立平面直角坐标系。
因为AB=6,AE=5,
所以OE=$\sqrt{AE^{2}-OA^{2}}=\sqrt{AE^{2}-(\frac{1}{2}AB)^{2}}=4$,
所以A(-3,0),B(3,0),C(3,-4),D(-3,-4),E(0,4)。

策略点拨
建立平面直角坐标系的基本思路
(1)分析条件,选择适当的点作为原点;
(2)过原点在两个互相垂直的方向上分别作出x轴和y轴;
(3)确定正方向和单位长度。
解题通法
建立平面直角坐标系的基本方法
(1)使图形中尽量多的点在坐标轴上。
(2)以某条特殊线段所在的直线为x轴或y轴,如三角形的高、中线等。
(3)以对称图形的对称轴为x轴或y轴。
(4)以某个已知点为原点,使其坐标为(0,0)。

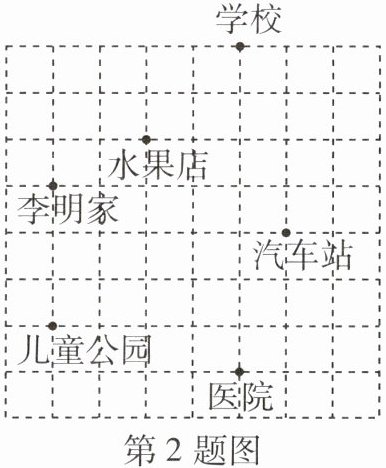
2 教材习题变式 [2025太原晋源区期末]如图是李明绘制的他所在社区的平面示意图,若学校所在位置的坐标是(1,4),儿童公园所在位置的坐标为(-3,-2),则位于(2,0)的建筑是 ( )


A. 汽车站
B. 医院
C. 李明家
D. 水果店

答案：
A 建立平面直角坐标系如图所示,可知位于(2,0)的建筑是汽车站。

3 新情境 [2025保定竞秀区期中]2025年第九届亚洲冬季运动会将在哈尔滨举行。如图是本届亚冬会的会徽“超越”,将其放在平面直角坐标系中,若A,C两点的坐标分别为(1,2),(-1,3),则点B的坐标为____。

答案：
(-2,-1) 由A,C两点的坐标分别为(1,2),(-1,3),建立平面直角坐标系如图所示,可得点B的坐标为(-2,-1)。

4 新趋势·传统文化 教材习题变式 [2025济宁任城区期末]围棋,起源于中国,古代称为“弈”,
直角坐标系求坐标
课时检测
是棋类鼻祖,距今已有4000多年的历史。如图是某围棋棋盘的局部,若棋盘是由边长均为1的小正方形组成的,棋盘上A,B两颗棋子的坐标分别为(-2,4),(1,2)。
(1)根据题意,画出相应的平面直角坐标系；
(2)分别写出C,D两颗棋子的坐标；
(3)有一颗黑色棋子E的坐标为(3,-1),请在图中画出黑色棋子E。

答案：
解:
(1)建立平面直角坐标系如图所示。

(2)棋子C的坐标为(2,1),棋子D的坐标为(-2,-1)。
(3)黑色棋子E如图所示。

5 在平面直角坐标系xOy中,点A的坐标为(-2,3),过点A作AB⊥x轴,垂足为点B,则△AOB的面积为____。

答案：
3 如图,根据题意可知AB⊥OB,AB=3,OB=2,所以$S_{\triangle AOB}=\frac{1}{2}\cdot AB\cdot OB=\frac{1}{2}\times3\times2=3$。

6 [2024郑州枫杨外国语学校月考]已知在平面直角坐标系中有三点A(-2,1),B(3,1),C(2,3)。请回答如下问题：
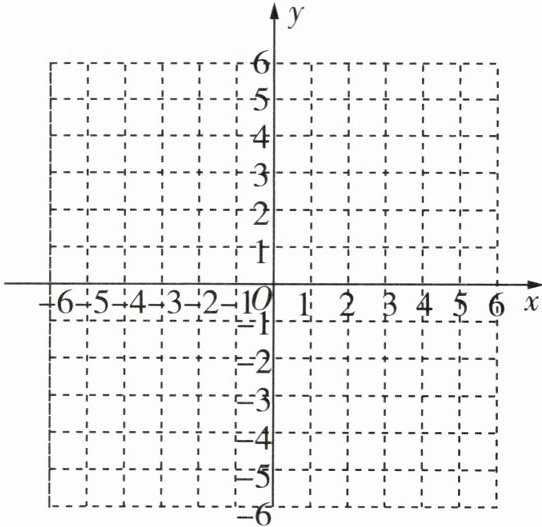
(1)在如图所示的平面直角坐标系内描出点A,B,C的位置。
(2)求出以A,B,C三点为顶点的三角形的面积。
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10？若存在,直接写出点P的坐标；若不存在,请说明理由。

答案：
解:
(1)点A,B,C的位置如图所示。

(2)如图,依题意,得AB//x轴,且AB=3-(-2)=5,
所以$S_{\triangle ABC}=\frac{1}{2}\times5\times2=5$。
(3)存在。点P的坐标为(0,5)或(0,-3)。
因为AB=5,$S_{\triangle ABP}=10$,
所以点P到AB的距离为4,
又因为点P在y轴上,
所以点P的坐标为(0,5)或(0,-3)。
名师点睛
数形结合思想主要体现在借助平面直角坐标系把几何问题转化为代数问题,同时也可以把代数问题转化为几何问题,每一个有序实数对都对应平面直角坐标系中的一个点,也可以用点的坐标来描述点及图形的位置。