《2025年一遍过八年级数学上册北师大版》

1 [2024陕西中考副卷]若点$A(-2,y_{1})和点B(2,y_{2})在同一个正比例函数y= kx(k＜0)$的图象上,则(A)
A.$y_{1}= -y_{2}$
B.$y_{1}= y_{2}$
C.$y_{2}＞0$
D.$y_{2}＞y_{1}$

答案： A 根据题意，得 $y_1 = -2k ＞ 0$，$y_2 = 2k ＜ 0$，故 C 项错误；$y_1 ＞ y_2$，故 D 项错误；$y_1 = -y_2$，故 B 项错误，A 项正确。

2 [2024临夏州中考]一次函数$y= kx-1(k≠0)$的函数值y随x的增大而减小,它的图象不经过的象限是(A)
A.第一象限
B.第二象限
C.第三象限
D.第四象限

答案： A 因为一次函数 $y = kx - 1(k \neq 0)$ 的函数值 $y$ 随 $x$ 的增大而减小，所以 $k ＜ 0$，又因为 $b = -1 ＜ 0$，(与 $y$ 轴交于负半轴)所以该函数图象经过第二、三、四象限，不经过第一象限。

在平面直角坐标系中,若一次函数的图象经过第一、二、三象限,请写出一个符合该条件的一次函数的表达式y = x + 1。

答案： (答案不唯一)$y = x + 1$ 设一次函数的表达式为 $y = kx + b(k \neq 0)$，因为一次函数的图象经过第一、二、三象限，所以 $k ＞ 0$，$b ＞ 0$，所以一次函数的表达式可以是 $y = x + 1$。

4 [2024淮安中考]一辆轿车从A地驶向B地,设出发xh后,这辆轿车离B地的路程为ykm,已知y与x之间的函数表达式为$y= 200-80x$,则轿车从A地到达B地所用时间是2.5h。

答案： 2.5 因为 $y = 200 - 80x$，令 $y = 0$，则 $200 - 80x = 0$，所以 $x = 2.5$，所以轿车从 $A$ 地到达 $B$ 地所用时间是 $2.5h$。

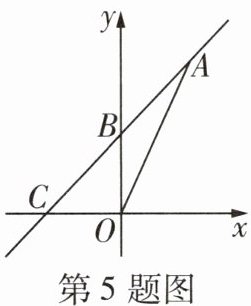
5 [2024凉山州中考]如图,一次函数$y= kx+b的图象经过A(3,6),B(0,3)$两点,交x轴于点C,则$\triangle AOC$的面积为____9。

答案： 9 因为一次函数 $y = kx + b$ 的图象经过 $A(3, 6)$，$B(0, 3)$ 两点，所以 $b = 3$，$3k + b = 6$，所以 $k = 1$，所以一次函数的表达式为 $y = x + 3$，当 $y = 0$ 时，$x = -3$，所以 $C(-3, 0)$，所以 $S_{\triangle AOC} = \frac{1}{2} × 3 × 6 = 9$。

6 [2024济南中考]某公司生产了A,B两款新能源电动汽车。如图,$l_{1},l_{2}$分别表示A款,B款新能源电动汽车充满电后电池的剩余电量$y(kW\cdot h)与汽车行驶路程x(km)$的关系。当两款新能源电动汽车的行驶路程都是300km时,A款新能源电动汽车电池的剩余电量比B款新能源电动汽车电池的剩余电量多____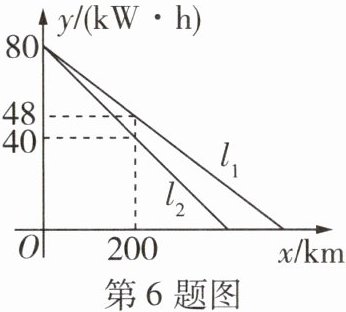12$kW\cdot h$。

答案： $A$ 款新能源电动汽车每千米的耗电量为 $(80 - 48) ÷ 200 = 0.16(kW \cdot h)$，$B$ 款新能源电动汽车每千米的耗电量为 $(80 - 40) ÷ 200 = 0.2(kW \cdot h)$，所以 $l_1$ 对应的函数表达式为 $y_1 = 80 - 0.16x$，$l_2$ 对应的函数表达式为 $y_2 = 80 - 0.2x$，当 $x = 300$ 时，$y_1 = 80 - 0.16 × 300 = 32$，$y_2 = 80 - 0.2 × 300 = 20$，$32 - 20 = 12(kW \cdot h)$，所以当两款新能源电动汽车的行驶路程都是 $300km$ 时，$A$ 款新能源电动汽车电池的剩余电量比 $B$ 款新能源电动汽车电池的剩余电量多 $12kW \cdot h$。

7 [新趋势·结论开放][2024攀枝花中考]如图,折线OABC表示了距离s(米)与时间t(分)之间的函数关系。
(1)分别直接写出线段OA,AB所对应的函数表达式,并注明相应的t的取值范围;
线段OA对应的函数表达式为s=45t(0≤t≤20)，线段AB对应的函数表达式为s=900(20≤t≤30)。
(2)请你想象一个符合函数图象的实际情境,并用语言进行描述(不必描述具体的速度)。
小明从家步行去图书馆，图书馆距离小明家900米，用时20分钟，然后小明在图书馆借书用了10分钟，再步行回家，用时15分钟

答案： 解：
(1)线段 $OA$ 对应的函数表达式为 $s = 45t(0 \leq t \leq 20)$，
线段 $AB$ 对应的函数表达式为 $s = 900(20 \leq t \leq 30)$。
(2)(答案不唯一，符合图象即可)小明从家步行去图书馆，图书馆距离小明家 $900$ 米，用时 $20$ 分钟，然后小明在图书馆借书用了 $10$ 分钟，再步行回家，用时 $15$ 分钟。

8 [2023温州中考]如图,在平面直角坐标系中,点$A(2,m)$在直线$y= 2x-\frac {5}{2}$上,过点A的直线交y轴于点$B(0,3)$。
(1)求m的值和直线AB的函数表达式;
m的值为$\frac{3}{2}$，直线AB的函数表达式为$y=-\frac{3}{4}x+3$
(2)若点$P(t,y_{1})$在线段AB上,点$Q(t-1,y_{2})$在直线$y= 2x-\frac {5}{2}$上,求$y_{1}-y_{2}$的最大值。
$y_{1}-y_{2}$的最大值为$\frac{15}{2}$

答案： 解：
(1)把点 $A(2, m)$ 的坐标代入 $y = 2x - \frac{5}{2}$ 中，得 $m = \frac{3}{2}$。
设直线 $AB$ 的函数表达式为 $y = kx + b$，把 $B(0, 3)$ 的坐标代入，得 $b = 3$，把 $A(2, \frac{3}{2})$ 的坐标代入，得 $k = -\frac{3}{4}$，
所以直线 $AB$ 的函数表达式为 $y = -\frac{3}{4}x + 3$。
(2)因为点 $P(t, y_1)$ 在线段 $AB$ 上，
所以 $y_1 = -\frac{3}{4}t + 3(0 \leq t \leq 2)$。
因为点 $Q(t - 1, y_2)$ 在直线 $y = 2x - \frac{5}{2}$ 上，
所以 $y_2 = 2(t - 1) - \frac{5}{2} = 2t - \frac{9}{2}$，
所以 $y_1 - y_2 = -\frac{3}{4}t + 3 - (2t - \frac{9}{2}) = -\frac{11}{4}t + \frac{15}{2}$。
因为 $-\frac{11}{4} ＜ 0$，所以 $y_1 - y_2$ 随 $t$ 的增大而减小，
所以当 $t = 0$ 时，$y_1 - y_2$ 的值最大，最大值为 $\frac{15}{2}$。