第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
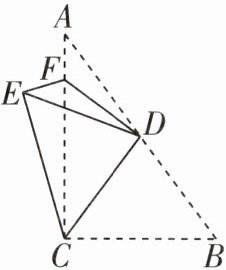
1 [2024常州田家炳中学期中]如图,在Rt△ABC中,∠ACB = 90°,AB = 10,BC = 6,点D为斜边AB的中点,连接CD,将△BCD沿CD翻折,使点B落在点E处,点F为直角边AC上一点,连接DF,将△ADF沿DF翻折,使点A与点E重合,则AF的长为______
$\frac{7}{4}$
。
答案:
$\frac{7}{4}$ 因为∠ACB = 90°,AB = 10,BC = 6,所以AC² = AB² - BC² = 64,所以AC = 8。由翻折可知,∠B = ∠DEC,∠A = ∠DEF,CE = BC = 6,AF = EF,因为∠A + ∠B = 90°,所以∠DEF + ∠DEC = 90°,即∠FEC = 90°,所以EF² + CE² = CF²,设AF = EF = x,则CF = AC - AF = 8 - x,所以x² + 6² = (8 - x)²,所以x = $\frac{7}{4}$。
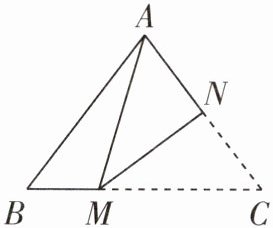
2 如图,在△ABC中,AB = AC = 5,BC = 6,点M,N分别在边BC,AC上,将△ABC沿MN折叠,使得点C与点A重合,求折痕MN的长。

答案:
解:如图,过点A作AD⊥BC于点D。
因为AB = AC = 5,BC = 6,
所以BD = CD = 3,所以AD = 4。
因为将△ABC沿MN折叠,使得点C与点A重合,
所以AM = CM,AN = $\frac{1}{2}$AC = $\frac{5}{2}$,MN⊥AC。
设AM = CM = x,则MD = x - 3,
在Rt△ADM中,由勾股定理,得AD² + MD² = AM²,
即4² + (x - 3)² = x²,解得x = $\frac{25}{6}$。
在Rt△AMN中,由勾股定理,
得MN² = AM² - AN² = ($\frac{25}{6}$)² - ($\frac{5}{2}$)² = $\frac{100}{9}$,
所以MN = $\frac{10}{3}$。

解:如图,过点A作AD⊥BC于点D。
因为AB = AC = 5,BC = 6,
所以BD = CD = 3,所以AD = 4。
因为将△ABC沿MN折叠,使得点C与点A重合,
所以AM = CM,AN = $\frac{1}{2}$AC = $\frac{5}{2}$,MN⊥AC。
设AM = CM = x,则MD = x - 3,
在Rt△ADM中,由勾股定理,得AD² + MD² = AM²,
即4² + (x - 3)² = x²,解得x = $\frac{25}{6}$。
在Rt△AMN中,由勾股定理,
得MN² = AM² - AN² = ($\frac{25}{6}$)² - ($\frac{5}{2}$)² = $\frac{100}{9}$,
所以MN = $\frac{10}{3}$。

3 [2025宝鸡一中调研]如图,折叠长方形的一边AD,使点D落在BC边上的F点处,若AB = 8 cm,BC = 10 cm,则EC的长为(
A. 2 cm
B. 3 cm
C. 4 cm
D. 5 cm
3cm
)A. 2 cm
B. 3 cm
C. 4 cm
D. 5 cm
答案:
B 由题意可知,DC = AB = 8cm,∠B = ∠C = 90°,AF = AD = 10cm,设EF = DE = xcm,则EC = (8 - x)cm,由勾股定理,得BF² = 10² - 8²,所以BF = 6cm,所以CF = 10 - 6 = 4(cm)。在Rt△EFC中,由勾股定理,得x² = 4² + (8 - x)²,解得x = 5,所以EC = 8 - 5 = 3(cm)。
4 [2025揭阳榕城区期中]如图,在长方形ABCD中,AB = 4,BC = 3,P为边BC上一点,将△CDP沿DP折叠,点C落在点E处,DE,PE分别交AB于点F,G,已知GE = GB,则BF的长为(
A. $\frac{17}{5}$
B. $\frac{3}{5}$
C. $\frac{12}{5}$
D. 5
$\frac{12}{5}$
)A. $\frac{17}{5}$
B. $\frac{3}{5}$
C. $\frac{12}{5}$
D. 5
答案:
4 C 由折叠知∠E = ∠C = 90°,EP = CP,DE = DC,在△GEF和△GBP中,$\left\{\begin{array}{l} ∠EGF = ∠BGP,\\ GE = GB,\\ ∠E = ∠B = 90^{\circ },\end{array}\right.$ 所以△GEF≌△GBP(ASA),
所以EF = BP,GF = GP,所以BF = EP = CP,设BF = EP = CP = x,则AF = 4 - x,EF = 3 - x,所以DF = 4 - (3 - x) = 1 + x,在Rt△ADF中,由勾股定理,得(4 - x)² + 3² = (1 + x)²,解得x = $\frac{12}{5}$,所以BF = $\frac{12}{5}$。
所以EF = BP,GF = GP,所以BF = EP = CP,设BF = EP = CP = x,则AF = 4 - x,EF = 3 - x,所以DF = 4 - (3 - x) = 1 + x,在Rt△ADF中,由勾股定理,得(4 - x)² + 3² = (1 + x)²,解得x = $\frac{12}{5}$,所以BF = $\frac{12}{5}$。
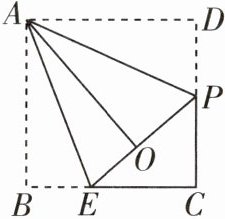
5 [2024贵阳一模改编]如图,动点E,P分别是正方形ABCD的边BC,CD上的动点,沿AE,AP折叠正方形,点B,D的对应点恰好都落在点O处,若AB = 3,当点P是CD边的三等分点时,BE的长为
$\frac{3}{2}$ 或 $\frac{3}{5}$
。
答案:
$\frac{3}{2}$ 或 $\frac{3}{5}$ 四边形ABCD是正方形,AB = 3,点P是CD边的三等分点,则分两种情况。若DP = 1,则PC = CD - DP = 3 - 1 = 2,设BE = x,则CE = 3 - x,由折叠可知,OE = BE = x,DP = OP = 1,所以PE = OE + OP = x + 1,在Rt△PCE中,PE² = PC² + CE²,即(x + 1)² = 2² + (3 - x)²,解得x = $\frac{3}{2}$,所以BE = $\frac{3}{2}$;若DP = 2,同理可得BE = $\frac{3}{5}$。
6 [2024揭阳惠城中学月考]如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B'处,点A落在点A'处。
(1)试说明B'E = BF;
(2)设AE = a,AB = b,BF = c,试猜想a,b,c之间的关系,并说明理由。
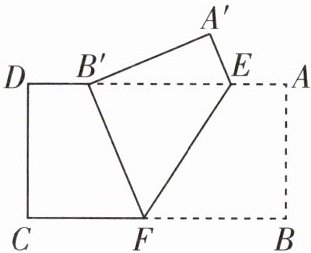
(1)由折叠的性质,得B'F = BF,∠B'FE = ∠BFE,
在长方形纸片ABCD中,AD//BC,
所以∠B'EF = ∠BFE,
所以∠B'FE = ∠B'EF,易得B'F = B'E,
所以B'E = BF。
(2)a,b,c之间的关系是
由(1)知B'E = BF = c,
由折叠的性质,得∠A' = ∠A = 90°,A'E = AE = a,A'B' = AB = b。
在△A'B'E中,A'E² + A'B'² = B'E²,所以a² + b² = c²。
(1)试说明B'E = BF;
(2)设AE = a,AB = b,BF = c,试猜想a,b,c之间的关系,并说明理由。

(1)由折叠的性质,得B'F = BF,∠B'FE = ∠BFE,
在长方形纸片ABCD中,AD//BC,
所以∠B'EF = ∠BFE,
所以∠B'FE = ∠B'EF,易得B'F = B'E,
所以B'E = BF。
(2)a,b,c之间的关系是
a² + b² = c²
。理由如下:由(1)知B'E = BF = c,
由折叠的性质,得∠A' = ∠A = 90°,A'E = AE = a,A'B' = AB = b。
在△A'B'E中,A'E² + A'B'² = B'E²,所以a² + b² = c²。
答案:
解:
(1)由折叠的性质,得B'F = BF,∠B'FE = ∠BFE,
在长方形纸片ABCD中,AD//BC,
所以∠B'EF = ∠BFE,
所以∠B'FE = ∠B'EF,易得B'F = B'E,
所以B'E = BF。
(2)a,b,c之间的关系是a² + b² = c²。理由如下:
由
(1)知B'E = BF = c,
由折叠的性质,得∠A' = ∠A = 90°,A'E = AE = a,A'B' = AB = b。
在△A'B'E中,A'E² + A'B'² = B'E²,所以a² + b² = c²。
(1)由折叠的性质,得B'F = BF,∠B'FE = ∠BFE,
在长方形纸片ABCD中,AD//BC,
所以∠B'EF = ∠BFE,
所以∠B'FE = ∠B'EF,易得B'F = B'E,
所以B'E = BF。
(2)a,b,c之间的关系是a² + b² = c²。理由如下:
由
(1)知B'E = BF = c,
由折叠的性质,得∠A' = ∠A = 90°,A'E = AE = a,A'B' = AB = b。
在△A'B'E中,A'E² + A'B'² = B'E²,所以a² + b² = c²。
查看更多完整答案,请扫码查看


