《2025年全品基础小练习高考数学》

1. [教材改编] 如图，为了测量河的两侧A，B两点之间的距离，在点A的同侧选取点C，测得∠ACB = 45°，∠BAC = 105°，AC = 50米，则A，B两点之间的距离为 ( )

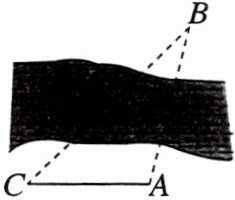
A. 100米
B. 50√3米
C. 25(√6 + √2)米
D. 50√2米

答案： D

2. 现要测量某河岸边A，B两地间的距离，如图，在B的正东方向选取一点C，测得CB = 2 km，A在C的西北方向上，且A在B的北偏东15°方向上，则A，B两地间的距离为 ( )

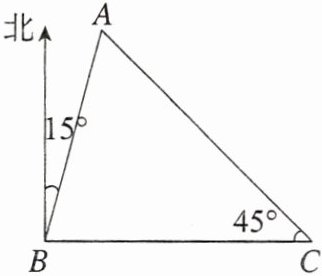
A. $\frac{2\sqrt{3}}{3}$ km
B. 2√3 km
C. $\frac{2\sqrt{6}}{3}$ km
D. 2√6 km

答案： C

3. 老虎甲在A地发现野鹿乙在北偏东15°方向上的B地，立刻以10√3 m/s的速度进行追捕，与此同时，野鹿乙以10√2 m/s的速度往北偏东75°方向逃跑，假设甲、乙都做匀速直线运动，且AB = 500(√6 - √2)m，则甲能够一次性捕获乙的最短时间为 ( )
A. 60 s
B. 80 s
C. 100 s
D. 120 s

答案： C

4. 位于某海域A处的甲船获悉，在其正东方向相距20 n mile的B处有一艘渔船遇险后抛锚等待营救，甲船立即前往救援，同时把消息告知位于甲船南偏西30°，且与甲船相距10 n mile的C处的乙船，乙船也立即前往营救渔船，则sin∠ACB = ( )
A. $\frac{\sqrt{21}}{7}$
B. $\frac{\sqrt{7}}{7}$
C. $\frac{\sqrt{3}}{7}$
D. $\frac{\sqrt{7}}{3}$

答案： A

5. 甲、乙两船分别位于某海域的A，B两处，且相距10海里，乙船在甲船南偏西45°方向上，乙船向正南方向行驶，甲船以乙船速度大小的√2倍沿直线追赶乙船，若甲船恰能追上乙船，则甲船行驶的方向为 ( )
A. 南偏西30°
B. 南偏西15°
C. 南偏东30°
D. 南偏东15°

答案： B

6. 我国油纸伞的制作工艺巧妙.如图①，伞不管是张开还是收拢，伞柄AP始终平分同一平面内两条伞骨所成的角(∠BAC)，且AB = AC，从而保证伞圈D能够沿着伞柄滑动.如图②，伞完全收拢时，伞圈D已滑动到D'的位置，且A，B，D'三点共线，AD' = 40 cm，B为AD'的中点，伞从完全张开到完全收拢，伞圈D沿着伞柄向下滑动的距离为24 cm，则当伞完全张开时，∠BAC的余弦值是 ( )

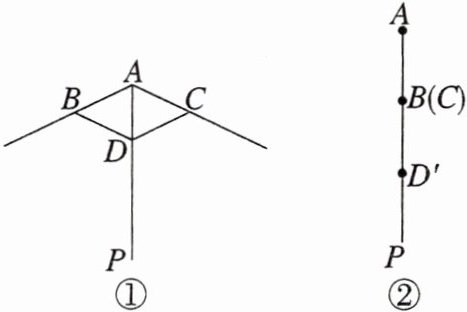
A. -$\frac{17}{25}$
B. -$\frac{4\sqrt{21}}{25}$
C. -$\frac{3}{5}$
D. -$\frac{8}{25}$

答案： A

7. 如图，某公园有A，B，C，D四棵桃树，其中∠DCA = 45°，∠CDB = ∠ADB = 30°，CD = (√6 + √2)m，∠ACB = 60°，则A，B两棵桃树间的距离是 ( )

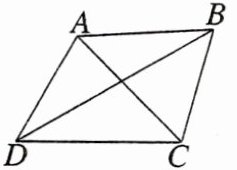
A. 4√3 m
B. √10 m
C. 6√2 m
D. 2√10 m

答案： B