第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 某地海拔$h$(单位:$km$)与温度$T$(单位:$^{\circ}C$)之间的关系可用$T = 23 - 5h$来表示,则该地区海拔为$3 km$的山顶上的温度为( )
A.$3^{\circ}C$
B.$8^{\circ}C$
C.$10^{\circ}C$
D.$13^{\circ}C$
A.$3^{\circ}C$
B.$8^{\circ}C$
C.$10^{\circ}C$
D.$13^{\circ}C$
答案:
B
2. 小陆同学和家人一同从家出发观看跳水比赛,由于距离较远,决定打车前往。已知出租车的收费标准是起步价$8.5$元(行程小于或等于$3 km$),超过$3 km每增加1 km$(不足$1 km按1 km$计算)加收$2$元,则出租车费$y$(单位:元)与行程$x$(单位:$km$,$x > 3$且为整数)之间的关系式为____。
答案:
$y=2x+2.5$
3. 为增强公民的节水意识,某市制订了如下用水标准:每户每月的用水量不超过$10 m^{3}$时,水价为每立方米$2$元;超过$10 m^{3}$时,超过的部分按每立方米$3$元收费。设该市居民李大妈家某月用水量为$x m^{3}$,交水费$y$元,请回答下列问题:
(1)若李大妈家$5月份用水8.5 m^{3}$,应交水费______元。
(2)若李大妈家$6月份交水费35$元,这个月李大妈家用水______$m^{3}$。
(3)根据题意完成表格。
|用水量$x/m^{3}$| $3$ | | $10$ | | $15$ | |
|水费$y/元$| | $10$ | | $26$ | | $38$ |

(1)若李大妈家$5月份用水8.5 m^{3}$,应交水费______元。
(2)若李大妈家$6月份交水费35$元,这个月李大妈家用水______$m^{3}$。
(3)根据题意完成表格。
|用水量$x/m^{3}$| $3$ | | $10$ | | $15$ | |
|水费$y/元$| | $10$ | | $26$ | | $38$ |

答案:
(1)17 (2)15 (3)5,12,16;6,20,35
【例1】某学校需租用一辆$50$座校车,咨询了$A$,$B$两家租车公司。$A$公司计费标准:按里程收费,每千米$12$元。$B$公司计费标准:每千米$8$元,另加基础服务费$300$元(不足$1 km按1 km$计算)。
(1)若用车里程为$25 km$,选择哪家公司的校车更划算?
(2)若用车里程为$60 km$,选择哪家公司的校车更划算?
(3)当用车里程为多少千米时,两家公司的租车费用相同?
解题关键 审题时注意明确计费结构,比较两家总费用时,数值小者更优。
(1)若用车里程为$25 km$,选择哪家公司的校车更划算?
(2)若用车里程为$60 km$,选择哪家公司的校车更划算?
(3)当用车里程为多少千米时,两家公司的租车费用相同?
解题关键 审题时注意明确计费结构,比较两家总费用时,数值小者更优。
答案:
(1)A 公司费用:$12×25=300$(元),B 公司费用:$8×25+300=200+300=500$(元),因为 300 元<500 元,所以 A 公司更划算。
(2)A 公司费用:$12×60=720$(元),B 公司费用:$8×60+300=480+300=780$(元),因为 720 元<780 元,所以 A 公司更划算。
(3)设里程为$x\ km$,列方程,$12x=8x+300$,解得$x=75$。当里程为 75 km 时,两家公司费用相同。
(1)A 公司费用:$12×25=300$(元),B 公司费用:$8×25+300=200+300=500$(元),因为 300 元<500 元,所以 A 公司更划算。
(2)A 公司费用:$12×60=720$(元),B 公司费用:$8×60+300=480+300=780$(元),因为 720 元<780 元,所以 A 公司更划算。
(3)设里程为$x\ km$,列方程,$12x=8x+300$,解得$x=75$。当里程为 75 km 时,两家公司费用相同。
【例2】某城市为鼓励节约用气,采用分档计费方式计算天然气费用。家庭年用气量及分档单价如下表:
|计费档|户年用气量$x/m^{3}$|单价/(元/$m^{3}$)|
|第一档| $0 < x \leq 500$ | $2.0$ |
|第二档| $500 < x \leq 1000$ | $2.5$ |
|第三档| $x > 1000$ | $3.0$ |
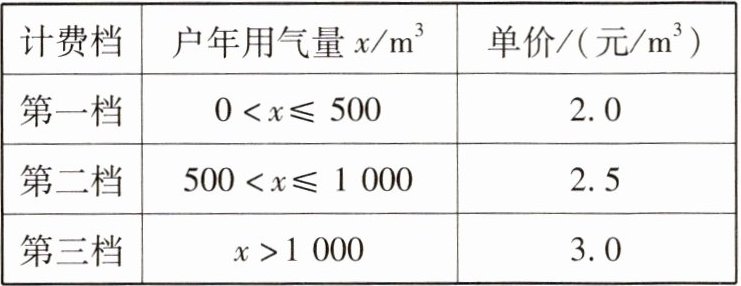
(1)当$500 < x \leq 1000$时,写出天然气费用$y$(单位:元)与$x$之间的关系式。
(2)某户一年用气量为$800 m^{3}$,求该户这一年的天然气费用。
(3)某户去年一年的天然气费用为$1500$元,求该户去年的用气量。
解题关键 第二档费用 = 第一档全部费用 + 超出部分费用。
|计费档|户年用气量$x/m^{3}$|单价/(元/$m^{3}$)|
|第一档| $0 < x \leq 500$ | $2.0$ |
|第二档| $500 < x \leq 1000$ | $2.5$ |
|第三档| $x > 1000$ | $3.0$ |

(1)当$500 < x \leq 1000$时,写出天然气费用$y$(单位:元)与$x$之间的关系式。
(2)某户一年用气量为$800 m^{3}$,求该户这一年的天然气费用。
(3)某户去年一年的天然气费用为$1500$元,求该户去年的用气量。
解题关键 第二档费用 = 第一档全部费用 + 超出部分费用。
答案:
(1)$y=500×2+(x-500)×2.5=2.5x$-250。
(2)当$x=800$时,$y=2.5×800-250=1750$(元)。所以该户这一年的天然气费用是 1750 元。
(3)因为$x=1000$时,费用为$2.5×1000-$250=2250 元>1500 元,所以用气量属于第二档。$2.5x-250=1500$,得$x=700$,所以该户去年用气量为$700\ m^3$。
(1)$y=500×2+(x-500)×2.5=2.5x$-250。
(2)当$x=800$时,$y=2.5×800-250=1750$(元)。所以该户这一年的天然气费用是 1750 元。
(3)因为$x=1000$时,费用为$2.5×1000-$250=2250 元>1500 元,所以用气量属于第二档。$2.5x-250=1500$,得$x=700$,所以该户去年用气量为$700\ m^3$。
查看更多完整答案,请扫码查看


