《2025年绩优学案八年级数学上册北师大版》

4. 在一张纸片(部分污损)上写有4个数字3,2,▲,5,若这4个数据的平均数为3,则这组数据的众数是____。

答案： 2

5. 小亮每天坚持体育锻炼,他记录了自己一周内每天锻炼的时间(单位:min),并制作了如图6-1-1-5所示的统计图。根据统计图,求小亮每天锻炼时间的众数和平均数。

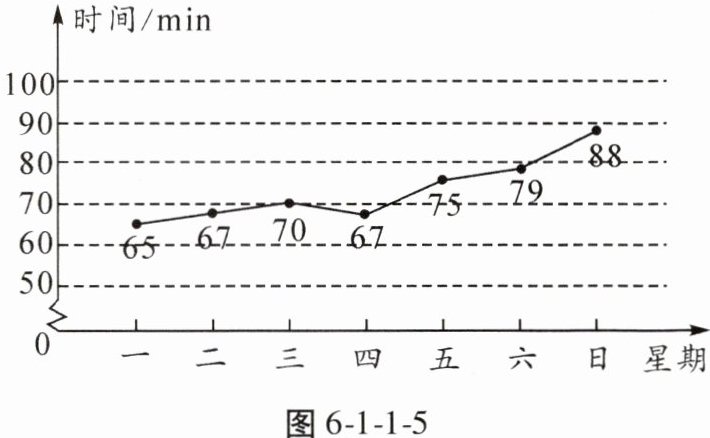
答案： 根据折线图小亮该周每天锻炼时间为(单位:min):65,67,70,67,75,79,88,$\overline {x}=\frac {1}{7}×(65+67+70+67+75+79+88)=73(min)$,这组数的众数是67 min,平均数是73 min。

6. 若1,2,3,a的平均数是3,又4,5,a,b的平均数是5,则a + b = ____,样本0,1,2,3,4,a,b的平均数是____。

答案： 11 3

7. 某中学八年级举行歌手大赛,其中八年级(1)、八年级(2)班派出的5名选手的比赛成绩如图6-1-1-6所示:

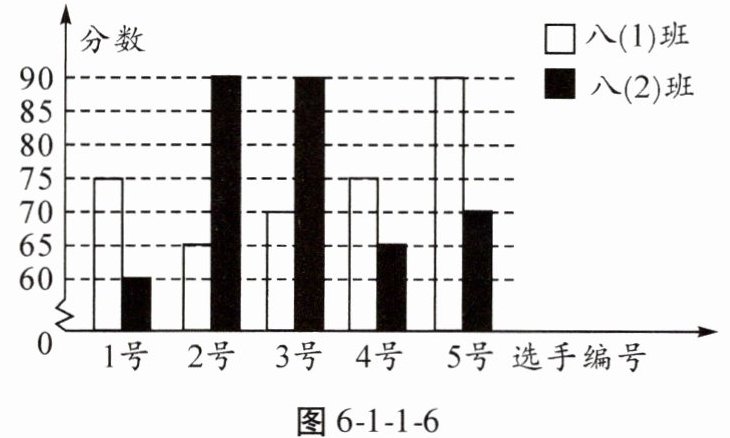
请计算两个班级5名选手比赛成绩的平均数和众数。

答案： 解:八
(1)的成绩分别是75,65,70,75,90,所以这组数据的众数是75,$\overline {x}=(75+65+70+75+90)÷5=75;$八
(2)的成绩分别是60,90,90,65,70,所以这组数据的众数是90,$\overline {x}=(60+90+90+65+70)÷5=75$。

8. 定义:对于两个正数a和b,a,b的算术平均数A = $\frac{a + b}{2}$,a,b的调和平均数H = $\frac{2}{\frac{1}{a} + \frac{1}{b}} = \frac{2ab}{a + b}$。
【观察归纳】(用“ ＜ ”“ = ”或“ ＞ ”填空)
①若a = 2,b = 4,则A____H;
②若a = $\frac{1}{3}$,b = $\frac{1}{5}$,则A____H;
③若a = 6,b = 6,则A____H;
【猜想验证】
①猜想:对于两个正数a和b,则A____H;(用“ ＜ ”“ = ”“ ＞ ”“ ≥ ”或“ ≤ ”填空)
②请验证你的猜想。

答案： 解:【观察归纳】①＞,②＞,③=;【猜想验证】①≥②证明:$A-H=\frac {a+b}{2}-\frac {2ab}{a+b}=\frac {(a+b)^{2}-4ab}{2(a+b)}=\frac {(a-b)^{2}}{2(a+b)}$,因为a和b是两个正数,所以$(a-b)^{2}≥0,2(a+b)＞0$,所以$\frac {(a-b)^{2}}{2(a+b)}≥0$,所以$A≥H$。