第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 某商场现销售某品牌运动套装,上衣和裤子一套售价 500 元。若将上衣价格下调 5%,将裤子价格上调 8%,则这样一套运动套装的售价提高 0.2%。设上衣和裤子在调价前单价分别为 x 元和 y 元,则可列方程组为 ( )
$A. \begin{cases}x + y = 500, \1 + 5\% )x + (1 - 8\% )y = 500×(1 + 0.2\% )\end{cases} $
$B. \begin{cases}x + y = 500, \1 - 5\% )x + (1 + 8\% )y = 500× 0.2\% \end{cases} $
$C. \begin{cases}x + y = 500, \1 - 5\% )x + (1 + 8\% )y = 500×(1 + 0.2\% )\end{cases} $
$D. \begin{cases}x + y = 500, \\5\% x + 8\% y = 500×(1 + 0.2\% )\end{cases} $
$A. \begin{cases}x + y = 500, \1 + 5\% )x + (1 - 8\% )y = 500×(1 + 0.2\% )\end{cases} $
$B. \begin{cases}x + y = 500, \1 - 5\% )x + (1 + 8\% )y = 500× 0.2\% \end{cases} $
$C. \begin{cases}x + y = 500, \1 - 5\% )x + (1 + 8\% )y = 500×(1 + 0.2\% )\end{cases} $
$D. \begin{cases}x + y = 500, \\5\% x + 8\% y = 500×(1 + 0.2\% )\end{cases} $
答案:
C
2. 小唐的爸爸用 800 元在大型药店购进普通医用口罩、N95 口罩,两种口罩共 100 个。该大型药店的普通医用口罩销售价为每个 2 元、N95 口罩销售价为每个 8 元,设购进普通医用口罩为 $ x $ 个,购进 N95 口罩为 $ y $ 个,可列出方程组为 ( )
A.$\begin{cases}x + y = 800, \\8x + 2y = 100\end{cases} $
B.$\begin{cases}x + y = 100, \\2x + 8y = 800\end{cases} $
C.$\begin{cases}x + y = 100, \\8x + 2y = 800\end{cases} $
D.$\begin{cases}x + y = 800, \\2x + 8y = 100\end{cases} $
A.$\begin{cases}x + y = 800, \\8x + 2y = 100\end{cases} $
B.$\begin{cases}x + y = 100, \\2x + 8y = 800\end{cases} $
C.$\begin{cases}x + y = 100, \\8x + 2y = 800\end{cases} $
D.$\begin{cases}x + y = 800, \\2x + 8y = 100\end{cases} $
答案:
B
3. 春节期间,某品牌服装店按标价打折销售,张某去该店买了两件衣服,第一件打 6 折,第二件打 5 折,共计 230 元,付款后,店主发现两件衣服的标价牌恰好挂反了,又找给了张某 20 元,设第一件衣服的原标价为 $ x $ 元,第二件衣服的原标价为 $ y $ 元,根据题意可列方程组为 。
答案:
$\left\{\begin{array}{l} 0.6x+0.5y=210,\\ 0.6y+0.5x=230\end{array}\right. $
【例 1】在当地农业技术部门指导下,小明家种植的菠萝获得丰收。去年菠萝的收入结余 12 000 元,今年菠萝的收入比去年增加了 20%,支出减少 10%,今年结余预计比去年多 11 400 元。
(1)填表:
|类别|收入/元|支出/元|结余/元|
|去年| $ x $ | $ y $ | |
|今年| | | |
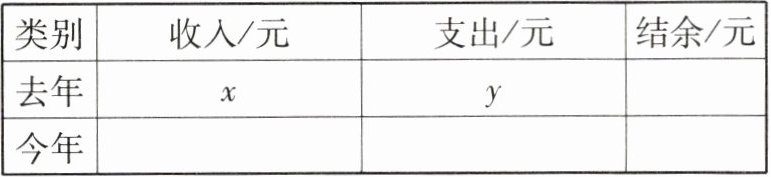
(用含 $ x $、$ y $ 的代数式表示)
(2)列方程组计算小明家今年种植菠萝的收入和支出。
解题关键 根据题意寻找包含全部题意的等量关系,通过设两个未知数,列二元一次方程组来解决。
(1)填表:
|类别|收入/元|支出/元|结余/元|
|去年| $ x $ | $ y $ | |
|今年| | | |

(用含 $ x $、$ y $ 的代数式表示)
(2)列方程组计算小明家今年种植菠萝的收入和支出。
解题关键 根据题意寻找包含全部题意的等量关系,通过设两个未知数,列二元一次方程组来解决。
答案:
解:
(1)12 000 $1.2x$ $0.9y$ 23 400
(2)由题意可得$\left\{\begin{array}{l} x-y=12000,\\ 1.2x-0.9y=23400,\end{array}\right. $
解得$\left\{\begin{array}{l} x=42000,\\ y=30000,\end{array}\right. $
则$1.2x=1.2×42000=50400,0.9y=0.9×30000=27000$。
答:小明家今年种植菠萝的收入和支出分别为 50 400 元、27 000 元。
(1)12 000 $1.2x$ $0.9y$ 23 400
(2)由题意可得$\left\{\begin{array}{l} x-y=12000,\\ 1.2x-0.9y=23400,\end{array}\right. $
解得$\left\{\begin{array}{l} x=42000,\\ y=30000,\end{array}\right. $
则$1.2x=1.2×42000=50400,0.9y=0.9×30000=27000$。
答:小明家今年种植菠萝的收入和支出分别为 50 400 元、27 000 元。
【例 2】某公司生产的一种营养品每千克含铁 42 mg,其原料信息如下表。已知甲食材每千克的进价是乙食材的 2 倍,购买 4 kg 的甲食材比购买 5 kg 的乙食材多花 60 元。
|原料|每千克含铁/mg|
|甲食材|50|
|乙食材|10|

(1)甲、乙两种食材每千克的进价分别是多少元?
(2)该公司每日用 18 000 元购进甲、乙两种食材并恰好全部用完,那么该公司每日购进甲、乙两种食材各多少千克?
解题关键 从表格中提取所需要的信息,找出等量关系列方程是解题关键。
|原料|每千克含铁/mg|
|甲食材|50|
|乙食材|10|

(1)甲、乙两种食材每千克的进价分别是多少元?
(2)该公司每日用 18 000 元购进甲、乙两种食材并恰好全部用完,那么该公司每日购进甲、乙两种食材各多少千克?
解题关键 从表格中提取所需要的信息,找出等量关系列方程是解题关键。
答案:
解:
(1)设乙食材每千克的进价为a元,则甲食材每千克的进价为$2a$元,由题意,得$4×2a-5×a=60,$
解得$a=20,$
则$2a=40$。
答:甲、乙两种食材每千克的进价分别是40 元、20 元。
(2)设该公司每日购进甲食材x kg,乙食材y kg,
由题意,得$\left\{\begin{array}{l} 40x+20y=18000,\\ 50x+10y=42(x+y),\end{array}\right. $
解得$\left\{\begin{array}{l} x=400,\\ y=100\end{array}\right. $。
答:该公司每日购进甲食材 400 kg,乙食材 100 kg。
(1)设乙食材每千克的进价为a元,则甲食材每千克的进价为$2a$元,由题意,得$4×2a-5×a=60,$
解得$a=20,$
则$2a=40$。
答:甲、乙两种食材每千克的进价分别是40 元、20 元。
(2)设该公司每日购进甲食材x kg,乙食材y kg,
由题意,得$\left\{\begin{array}{l} 40x+20y=18000,\\ 50x+10y=42(x+y),\end{array}\right. $
解得$\left\{\begin{array}{l} x=400,\\ y=100\end{array}\right. $。
答:该公司每日购进甲食材 400 kg,乙食材 100 kg。
查看更多完整答案,请扫码查看


