《2025年绩优学案八年级数学上册北师大版》

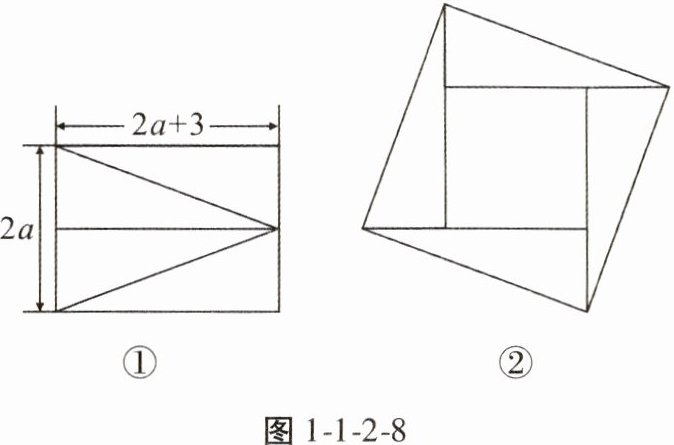
5. 如图1-1-2-8①,将长为2a+3,宽为2a的长方形分割成四个全等的直角三角形,拼成“赵爽弦图”(如图1-1-2-8②),得到大小两个正方形。
(1) 用关于a的代数式表示图②中小正方形的边长。
(2) 当a= 3时,求：图1-1-2-8②中大正方形的面积。

答案： 解：
(1)因为直角三角形较短的直角边长为$\frac{1}{2}×2a=a$，较长的直角边长为$2a+3$，所以小正方形的边长为$2a+3 - a=a+3$。
(2)当$a=3$时，大正方形的面积为$(2×3+3)^{2}+3^{2}=90$。

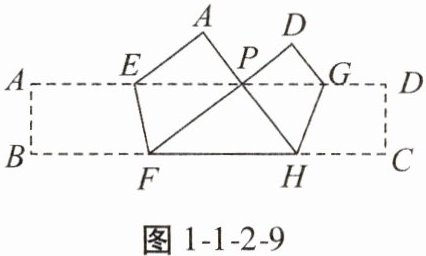
6. 如图1-1-2-9,把长方形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P点处,若∠FPH= 90°,PF= 8,PH= 6,则长方形ABCD的边BC长为( )

答案： C

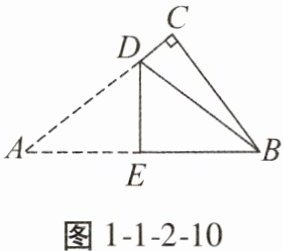
7. 如图1-1-2-10,已知Rt△ABC中,∠C= 90°,AC= 4cm,BC= 3cm。现将△ABC进行折叠,使顶点A,B重合,则折痕DE= cm。

答案： $\frac{15}{8}$

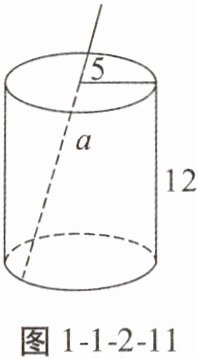
8. 如图1-1-2-11是一个圆柱形饮料罐,底面半径是5,高是12,上底面中心有一个小圆孔,插入一根到达底部的直吸管,请求出直吸管在罐内部分的长度a的范围(罐壁的厚度和小圆孔的大小忽略不计)。

答案： 解：当吸管底部在圆柱底面圆的圆心时，吸管在罐内部分的长度$a$最短，此时$a$为圆柱的高，即$a=12$。当吸管底部在圆柱底面圆的直径一侧端点时，吸管在罐内部分的长度$a$最长，因为$5^{2}+12^{2}=13^{2}$，所以$a=13$，故$12\leqslant a\leqslant13$。

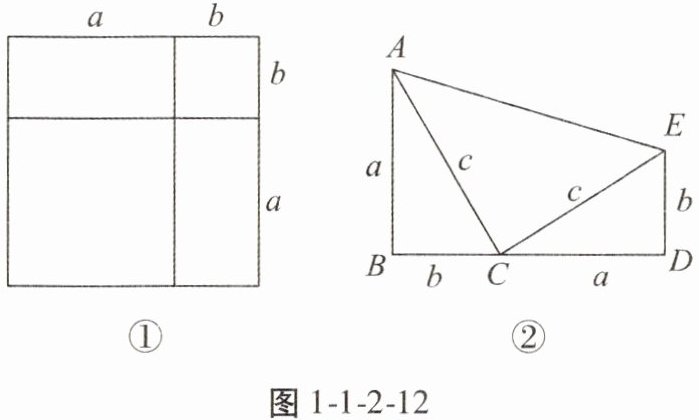
9. 【提出问题】如图1-1-2-12①是一个重要公式的几何解释。请你写出这个公式。
【解决问题】如图1-1-2-12②,Rt△ABC和Rt△CDE全等,∠B= ∠D= 90°,且B,C,D三点共线。试说明∠ACE= 90°。
【应用迁移】伽菲尔德利用上述的公式和图②证明了勾股定理,现请你尝试写出该证明过程。

答案：
解：[提出问题]这个公式为$(a + b)^{2}=a^{2}+2ab+b^{2}$。[解决问题]因为$Rt\triangle ABC$和$Rt\triangle CDE$全等，所以$\angle BAC=\angle DCE$。所以$\angle ACB+\angle DCE=\angle ACB+\angle BAC=90^{\circ}$。由于$B,C,D$共线，所以$\angle ACE=180^{\circ}-(\angle ACB+\angle DCE)=180^{\circ}-90^{\circ}=90^{\circ}$。[应用迁移]梯形$ABDE$的面积为$\frac{1}{2}(AB+ED)\cdot BD=\frac{1}{2}(a + b)(a + b)=\frac{1}{2}(a + b)^{2}$；梯形$ABDE$可分成三个直角三角形，其面积可以表示为$\frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2}$。所以$\frac{1}{2}(a + b)^{2}=\frac{1}{2}ab+\frac{1}{2}ab+\frac{1}{2}c^{2}$，即$a^{2}+b^{2}=c^{2}$。