《2025年绩优学案八年级数学上册北师大版》

7. “绿水青山就是金山银山”, 2025 年 3 月 12 日是我国第 45 个植树节, 某班组织学生在某园林基地进行植树活动, 活动开始前对若干棵树苗进行分配, 若 4 人合作种植一棵树苗, 则还剩 3 棵; 若 3 人合作种植一棵树苗, 则还有 2 人未分到树苗, 问共有多少棵树苗, 多少名学生。

答案： 解:设共有x棵树苗,y名学生,由题意,得$\left\{\begin{array}{l} \frac {y}{4}+3=x,\\ \frac {y-2}{3}=x,\end{array}\right.$解得$\left\{\begin{array}{l} x=14,\\ y=44。\end{array}\right.$答:共有14棵树苗,44名学生。

8. 如图, 在长方形 $ ABCD $ 中, 放入 6 个形状、大小都相同的小长方形, 所标尺寸如图所示。

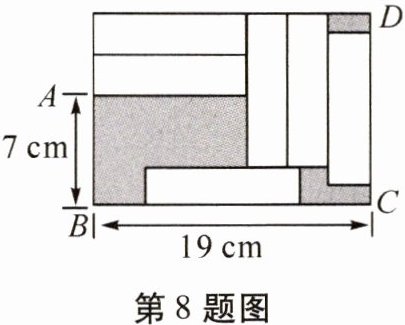
(1) 小长方形的长和宽各是多少?
(2) 求阴影部分的面积。

答案：
(1)设小长方形的长为x cm,宽为y cm,根据图形可知$\left\{\begin{array}{l} x+3y=19,\\ x+y=2y+7\end{array}\right.$解得$\left\{\begin{array}{l} x=10,\\ y=3。\end{array}\right.$答:小长方形的长为10 cm,宽为3 cm。
(2)由
(1)得小长方形的长为10 cm,宽为3 cm,所以大长方形的宽为13 cm,则阴影部分的面积=大长方形的面积-6个小长方形的面积=13×19-6×3×10=67($cm^{2}$)。答:阴影部分的面积为67 $cm^{2}$。

9. 甲、乙两人从 $ P $ 地出发沿同一条公路匀速前往 $ Q $ 地, 甲开汽车, 乙骑自行车。乙行驶的时间为 $ t(\mathrm{h}) $, 甲乙两人之间的距离为 $ y(\mathrm{km}) $, $ y $ 与 $ t $ 的函数关系如图所示, 乙先出发 1 h, 甲出发 0.5 h 与乙相遇。

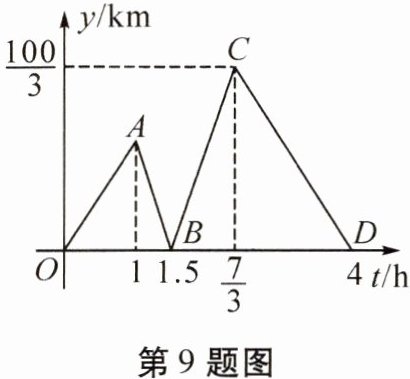
(1) 求出线段 $ BC $ 所在直线的函数表达式 (不需要写出自变量的取值范围);
(2) 写出 $ B $ 点的实际意义;
(3) 求甲、乙两人行驶的速度。

答案：
(1)由题意,设直线BC的函数表达式为y=kx+b,把(1.5,0),$(\frac {7}{3},\frac {100}{3})$代入,得$\left\{\begin{array}{l} 1.5k+b=0,\\ \frac {7}{3}k+b=\frac {100}{3},\end{array}\right.$所以$\left\{\begin{array}{l} k=40,\\ b=-60。\end{array}\right.$所以直线BC的函数表达式为y=40x-60。
(2)由题意,结合图象可得,B表示两人在乙出发1.5 h后两人相遇。
(3)由题意,设甲、乙两人行驶的速度分别是x km/h、y km/h,根据题意可得,$\left\{\begin{array}{l} 0.5x=(1+0.5)y,\\ (\frac {7}{3}-1)x-\frac {7}{3}y=\frac {100}{3},\end{array}\right.$解得$\left\{\begin{array}{l} x=60,\\ y=20。\end{array}\right.$答:甲的速度是60 km/h,乙的速度是20 km/h。