《2025年绩优学案八年级数学上册北师大版》

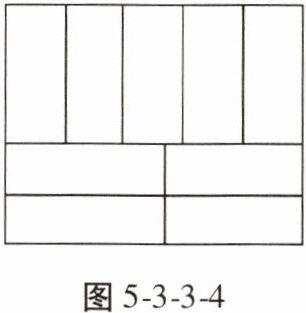
5. 学校为了提高绿化品位,美化环境,准备将一块周长为 $76$ m 的长方形草地,设计分成长和宽分别相等的 $9$ 块小长方形,(放置位置如图 5-3-3-4),种上各种花卉。经市场预测,绿化每平方米造价约为 $108$ 元。
(1)求出每一个小长方形的长和宽。
(2)请计算完成这项绿化工程预计投入资金多少元？

答案： 解:
(1)设小长方形的宽为x m,长为y m。则$\left\{\begin{array}{l} 2(y+2x+5x)=76,\\ 5x=2y,\end{array}\right. $解得$\left\{\begin{array}{l} x=4,\\ y=10\end{array}\right. $。答:每个小长方形的长和宽分别是10 m、4 m。
(2)$10×4×9×108=38880$(元),答:完成这块绿化工程预计投入资金为38880元。

6. 将 $9$ 个不同的整数填入表格中,使得每行、每列、每条对角线上的三个数之和都相等,则 $a$ 和 $b$ 的值分别是( )

A.$a = -4$,$b = 3$
B.$a = -4$,$b = -3$
C.$a = 4$,$b = 3$
D.$a = 4$,$b = -3$

答案： C

7. 甲、乙两车分别从相距 $210$ km 的 A,B 两地相向而行。
(1)两车均保持匀速行驶且甲车的速度是乙车速度的 $2$ 倍,若甲车比乙车提前 $2$ h 出发,则甲车出发后 $3$ h 两车相遇。求甲、乙两车的速度分别是多少(单位：km/h)？
(2)如果甲、乙两车保持(1)中的速度,同时出发相向而行,求经过多少小时两车相距 $30$ km。

答案： 解:
(1)设甲车的速度是x km/h,乙车的速度是y km/h,根据题意,得$\left\{\begin{array}{l} x=2y,\\ 3x+(3-2)y=210,\end{array}\right. $解得$\left\{\begin{array}{l} x=60,\\ y=30\end{array}\right. $。答:甲车的速度是60 km/h,乙车的速度是30 km/h。
(2)设经过t小时两车相距30 km。根据题意,得当两车第一次相距30 km时,$60t+30t=210-30$,解得$t=2$,当两车第二次相距30 km时,$60t+30t=210+30$,解得$t=\frac {8}{3}$,答:经过2 h或$\frac {8}{3}h$两车相距30 km。

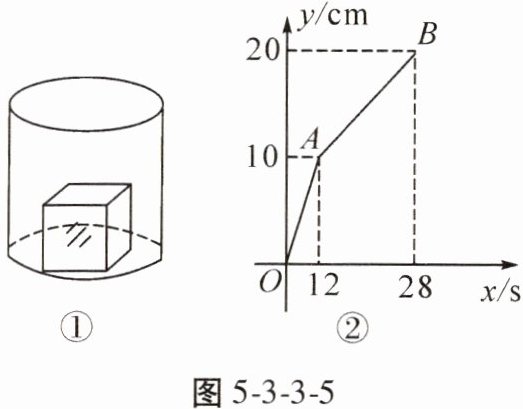
8. 如图 5-3-3-5①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,$28$ s 时注满水槽,水槽内水面的高度 $y$(cm)与注水时间 $x$(s)之间的函数图象如图②所示。如果将正方体铁块取出,又经过多少秒恰好将水槽注满,此水槽的底面面积为多少平方厘米？

答案： 解:由题意可得,12 s时,水槽内水面的高度为10 cm,12 s后水槽内水面高度变化趋势改变,所以正方体的棱长为10 cm,因为没有立方体时,水面上升从10 cm到20 cm,所用的时间为$28-12=16(s),$前12 s由于立方体的存在,导致水面上升速度加快了4 s,所以将正方体铁块取出,又经过4 s恰好将此水槽注满。根据题意:正方体的体积为$10^{3}=1000(cm^{3}),$设注水的速度为$vcm^{3}/s$,圆柱的底面积为$s cm^{2}$,根据题意,得$\left\{\begin{array}{l} 12v+1000=10s,\\ 28v+1000=20s,\end{array}\right. $解得$\left\{\begin{array}{l} v=250,\\ s=400\end{array}\right. $。所以水槽的底面面积为$400cm^{2}$。