《2025年绩优学案八年级数学上册北师大版》

1. 若一艘轮船沿江水顺流航行 $120$ km 需用 $3$ h,它沿江水逆流航行 $60$ km 也需用 $3$ h,设这艘轮船在静水中的航速为 $x$ km/h,江水的流速为 $y$ km/h,则根据题意可列方程组为( )

A.$\begin{cases}3x - y = 60\\3x + y = 120\end{cases} $
B.$\begin{cases}3(x + y) = 120\\3(x - y) = 60\end{cases} $
C.$\begin{cases}3(x - y) = 120\\3(x + y) = 60\end{cases} $
D.$\begin{cases}3x + y = 60\\3x - y = 120\end{cases} $

答案： B

2. 如图 5-3-3-1,用形状、大小完全相同的小长方形墙砖拼成一个大长方形,设每个小长方形墙砖长和宽分别为 $x$ cm 和 $y$ cm,则依题意可列方程组为( )

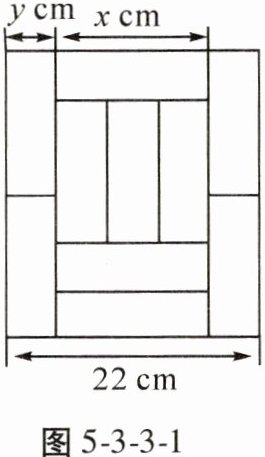
A.$\begin{cases}x + 2y = 22\\y = 3x\end{cases} $

B.$\begin{cases}2x + y = 22\\x = 3y\end{cases} $
C.$\begin{cases}x + 2y = 22\\5y = 22\end{cases} $
D.$\begin{cases}2x + y = 22\\5y = 22\end{cases} $

答案： C

3. 已知一个两位数,它的十位上的数字与个位上的数字和是 $9$,若颠倒个位数字与十位数字的位置,得到的新数比原数小 $63$,则这个两位数为( )

A.$28$
B.$82$
C.$18$
D.$81$

答案： D

【例 1】学校组织学生乘汽车去自然保护区野营,前 $\frac{1}{3}$ 路段为平路,其余路段为坡路。已知汽车在平路上行驶的速度为 $60$ km/h,在坡路上行驶的速度为 $30$ km/h。汽车从学校到自然保护区一共行驶了 $6.5$ h,求汽车在平路和坡路上各行驶了多长时间？
解题关键 本题考查的是二元一次方程组的应用,通过画线段图寻找等量关系建立方程组求解即可。

答案： 解:设汽车在平路上行驶了x h,在坡路上行驶了y h,由题意,得$\left\{\begin{array}{l} x+y=6.5,\\ 60x=\frac {1}{3}(60x+30y),\end{array}\right. $解得$\left\{\begin{array}{l} x=1.3,\\ y=5.2\end{array}\right. $。答:汽车在平路上行驶了1.3 h,在坡路上行驶了5.2 h。

【例 2】一个两位数,个位上的数字与十位上的数字的和为 $13$,若把个位上的数字与十位上的数字对调,则所得的数比原数的 $2$ 倍小 $4$,求原来的两位数。
解题关键 根据题意寻找等量关系列出二元一次方程组,由此得到答案。

答案： 解:根据题意设个位数字为x,十位数字为y,所以$\left\{\begin{array}{l} x+y=13,\\ 2(10y+x)-(10x+y)=4,\end{array}\right. $解得$\left\{\begin{array}{l} x=9,\\ y=4\end{array}\right. $。原来的两位数为$4×10+9=49$。