《2025年绩优学案八年级数学上册北师大版》

4. 若长方形的长为$(\sqrt{32}+\sqrt{8}) cm$,宽为$\sqrt{8} cm$,则此长方形的面积为____$cm^2$。

答案： 24

5. 计算：
(1)$2\sqrt{12}-6\sqrt{\frac{1}{3}}+2\sqrt{48}$；
(2)$\sqrt{27}×\sqrt{50}÷\sqrt{6}$；
(3)$(\sqrt{5}+\sqrt{2})(\sqrt{5}-\sqrt{2})+(\sqrt{3}-\sqrt{2})^{2}$。

答案：
(1)原式$=2×2\sqrt{3}-6×\frac{\sqrt{3}}{3}+2×4\sqrt{3}=4\sqrt{3}-2\sqrt{3}+8\sqrt{3}=10\sqrt{3}$;
(2)原式$=\sqrt{27×50÷6}=\sqrt{\frac{27×50}{6}}=\sqrt{9×25}=\sqrt{9}×\sqrt{25}=3×5=15$;
(3)原式$=(\sqrt{5})^{2}-(\sqrt{2})^{2}+(\sqrt{3})^{2}-2×\sqrt{3}×\sqrt{2}+(\sqrt{2})^{2}=5-2+3-2\sqrt{6}+2=8-2\sqrt{6}$。

6. 化简$\sqrt{-a^{3}}$的结果是( )

A.$a\sqrt{a}$
B.$-a\sqrt{a}$
C.$a\sqrt{-a}$
D.$-a\sqrt{-a}$

答案： D

7. 对于任意不相等的两个实数a,b,新定义一种运算“$*$”如下：$a*b= \frac{\sqrt{a}×\sqrt{b}}{\sqrt{b}-a-1}$,则$2*6= $____。

答案： 2

8. 如图2-3-3-1,某小区有一块长方形空地ABCD,长BC为$\sqrt{72} m$,宽AB为$\sqrt{32} m$,现要在空地中间修建一个小长方形花坛(阴影部分),花坛的长为$(\sqrt{10}+1) m$,宽为$(\sqrt{10}-1) m$。

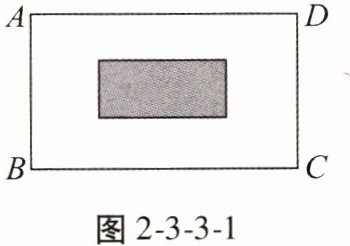
(1)求长方形空地的周长；
(2)长方形空地上花坛以外的部分拟修建成休闲区,此休闲区地面上要铺设造价为20元/$m^2$的地砖,铺设完整个休闲区,购买地砖需要花费多少元？

答案：
(1)$(\sqrt{72}+\sqrt{32})×2=(6\sqrt{2}+4\sqrt{2})×2=10\sqrt{2}×2=20\sqrt{2}(m)$。答:长方形空地的周长为$20\sqrt{2}\ m$。
(2)$\sqrt{72}×\sqrt{32}-(\sqrt{10}+1)×(\sqrt{10}-1)=6\sqrt{2}×4\sqrt{2}-(10-1)=48-9=39(m^{2})$,$20×39=780$(元)。答:购买地砖需要花费780元。

9. 已知$a= \frac{1}{2+\sqrt{3}}$,求$2a^{2}-8a+1$的值。
小明是这样解答的：
解：因为$a= \frac{1}{2+\sqrt{3}}= \frac{2-\sqrt{3}}{(2+\sqrt{3})(2-\sqrt{3})}= 2-\sqrt{3}$,所以$a - 2 = -\sqrt{3}$。所以$(a - 2)^{2}= 3$,即$a^{2}-4a + 4 = 3$,所以$a^{2}-4a = -1$。所以$2a^{2}-8a + 1 = 2(a^{2}-4a)+1 = 2×(-1)+1 = -1$。
请根据小明的解答过程,解决下列问题：
(1)化简：$\frac{1}{\sqrt{2}+1}= $____；
(2)计算：$\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{3}+\sqrt{2}}+\frac{1}{\sqrt{4}+\sqrt{3}}+…+\frac{1}{\sqrt{2026}+\sqrt{2025}}$；
(3)若$a= \frac{1}{3 + 2\sqrt{2}}$,求$3a^{2}-18a + 1$的值。

答案：
(1)$\sqrt{2}-1$
(2)原式$=(\sqrt{2}-1)+(\sqrt{3}-\sqrt{2})+(\sqrt{4}-\sqrt{3})+\cdots+(\sqrt{2026}-\sqrt{2025})=\sqrt{2026}-1$。
(3)因为$a=\frac{1}{3+2\sqrt{2}}=3-2\sqrt{2}$,所以$a-3=-2\sqrt{2}$。所以$(a-3)^{2}=8$,即$a^{2}-6a+9=8$,所以$a^{2}-6a=-1$。所以$3a^{2}-18a+1=3(a^{2}-6a)+1=3×(-1)+1=-2$。