第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
7. 在弹性限度内,弹簧长度 $ y $(单位:cm)与所挂物体质量 $ x $(单位:kg)之间的关系式为 $ y= 0.5x+14.5 $,当弹簧长度为18cm时,弹簧所挂物体的质量为______kg。
答案:
7
8. 一种豆子每千克售价为2元,豆子的总售价 $ y $(单位:元)与售出豆子的质量 $ x $(单位:kg)之间的关系如下表:
|售出豆子的质量x/kg|0.5|1|1.5|2|2.5|5|
|总售价y/元|1|2|3|4|5|10|
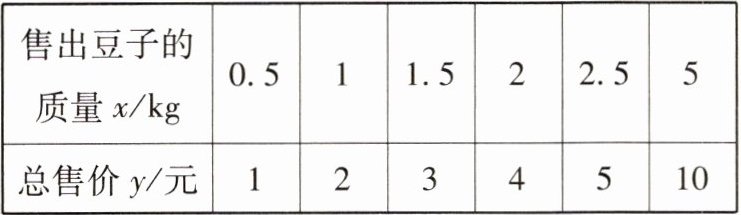
(1)这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是对应的函数值?
(2)当豆子售出5kg时,总售价是多少?
(3)按表中给出的关系,用一个式子把 $ x $ 与 $ y $ 之间的关系表示出来;
(4)当豆子售出20kg时,总售价是多少?
|售出豆子的质量x/kg|0.5|1|1.5|2|2.5|5|
|总售价y/元|1|2|3|4|5|10|

(1)这个表格中反映的是哪两个变量之间的关系?哪个是自变量?哪个是对应的函数值?
(2)当豆子售出5kg时,总售价是多少?
(3)按表中给出的关系,用一个式子把 $ x $ 与 $ y $ 之间的关系表示出来;
(4)当豆子售出20kg时,总售价是多少?
答案:
解:
(1)这个表格中反映的是总售价与售出豆子的质量之间的关系,自变量是售出豆子的质量,对应的函数值是总售价。
(2)由表格信息可得,豆子售出5 kg的总售价为10元。
(3)因为总售价等于单价乘以数量,所以y=2x。
(4)把x=20代入y=2x,得y=2×20=40,即当豆子售出20 kg时,总售价为40元。
(1)这个表格中反映的是总售价与售出豆子的质量之间的关系,自变量是售出豆子的质量,对应的函数值是总售价。
(2)由表格信息可得,豆子售出5 kg的总售价为10元。
(3)因为总售价等于单价乘以数量,所以y=2x。
(4)把x=20代入y=2x,得y=2×20=40,即当豆子售出20 kg时,总售价为40元。
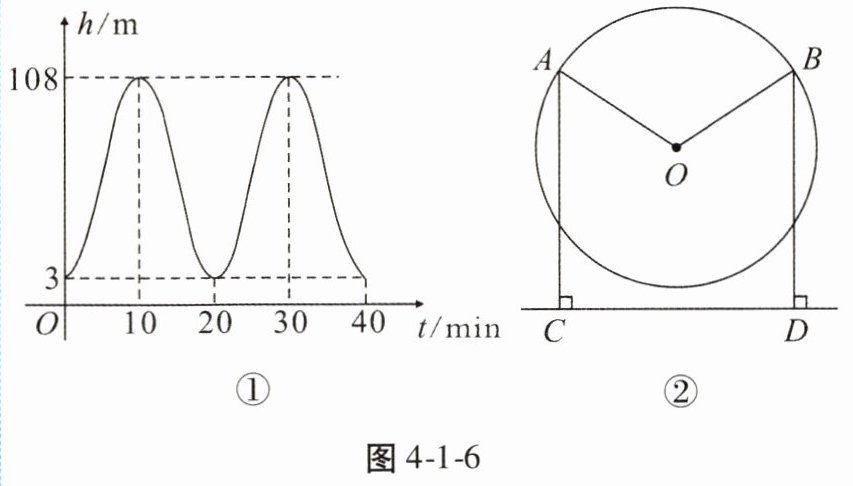
9. 数学活动课上老师提到我们身边很多事物都蕴含着数学知识,班上的数学兴趣小组决定趁着游玩时对摩天轮进行实地调研。摩天轮位于儿童公园内,摩天轮上均匀分布着60个吊舱,顺时针旋转一周需要20min。小组成员使用秒表和手机的测距功能,记录某个吊舱从最低点旋转到不同位置时距地面的高度 $ h $(m)和所用的时间 $ t $(min)的数据,并绘制变化图如图4-1-6①。
请根据图4-1-6①中的信息回答:
(1)在这个变化过程中,变量是______;
(2)摩天轮最高点距地面______m,摩天轮最低点距地面______m;
(3)如图4-1-6②,摩天轮某个吊舱从点 $ A $ 顺时针旋转到点 $ B $ 需6min,请你求出这个吊舱从点 $ A $ 顺时针旋转到点 $ B $ 所走的路径的长度。(结果保留 $ \pi $)
请根据图4-1-6①中的信息回答:
(1)在这个变化过程中,变量是______;
(2)摩天轮最高点距地面______m,摩天轮最低点距地面______m;
(3)如图4-1-6②,摩天轮某个吊舱从点 $ A $ 顺时针旋转到点 $ B $ 需6min,请你求出这个吊舱从点 $ A $ 顺时针旋转到点 $ B $ 所走的路径的长度。(结果保留 $ \pi $)

答案:
解:
(1)t,h
(2)108 3
(3)因为摩天轮最高点距地面108 m,最低点距离地面3 m,所以摩天轮的直径是105 m,所以105π÷20×6=63/2π(m)。
答:所走的路径的长度是63/2π m。
(1)t,h
(2)108 3
(3)因为摩天轮最高点距地面108 m,最低点距离地面3 m,所以摩天轮的直径是105 m,所以105π÷20×6=63/2π(m)。
答:所走的路径的长度是63/2π m。
查看更多完整答案,请扫码查看


