第143页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
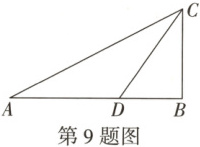
9. 如图,在 $Rt\triangle ABC$ 中,$\angle B = 90^{\circ}$,$D$ 为 $AB$ 上一点,$AD = CD$.
(1)尺规作图:以 $AC$ 为对角线作菱形 $ADCE$;
(2)在(1)的条件下,连接 $DE$,若 $\tan\angle CAB = \frac{1}{2}$,$DE = 2$,求 $BC$ 的长.
(1)尺规作图:以 $AC$ 为对角线作菱形 $ADCE$;
(2)在(1)的条件下,连接 $DE$,若 $\tan\angle CAB = \frac{1}{2}$,$DE = 2$,求 $BC$ 的长.

答案:
9. 解:
(1)如解图,菱形ADCE即为所求(作法不唯一);

(2)BC的长为$\frac{4\sqrt{5}}{5}$.
9. 解:
(1)如解图,菱形ADCE即为所求(作法不唯一);

(2)BC的长为$\frac{4\sqrt{5}}{5}$.
10. 在学习了等腰三角形和全等三角形的相关知识后,某数学兴趣小组发现了重要的事实:在等腰三角形底边上任取一点,向两腰作垂线段,这两条垂线段之和始终为一固定值.
请根据他们的想法与思路,完成下列作图和填空:
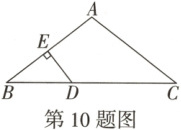
(1)如图,在 $\triangle ABC$ 中,$AB = AC$,$D$ 是 $BC$ 边上一点,$DE\perp AB$ 于点 $E$. 用尺规过点 $D$ 作 $AC$ 的垂线交 $AC$ 于点 $F$ (不写作法,保留作图痕迹);
(2)已知:在 $\triangle ABC$ 中,$AB = AC$,$D$ 是 $BC$ 边上一点,$DE\perp AB$ 于点 $E$,$DF\perp AC$ 于点 $F$,求证:$DE + DF$ 为一固定值.
证明:过点 $B$ 作 $BH\perp AC$ 交 $CA$ 的延长线于点 $H$,过点 $D$ 作 $DG\perp BH$ 于点 $G$.
$\because DF\perp AC$,
$\therefore \angle DGH = \angle GHF = \angle DFH = 90^{\circ}$,
$\therefore$ 四边形 $DFHG$ 是
$\therefore GH = DF$.
$\because DE\perp AB$,
$\therefore \angle BGD = \angle BED = 90^{\circ}$.
$\because AB = AC$,
$\therefore \angle ABC = \angle ACB$.
$\because \angle ACB + \angle GBD = 90^{\circ}$,$\angle ABC + \angle EDB = 90^{\circ}$,
$\therefore \underline{②}$.
在 $\triangle GBD$ 和 $\triangle EDB$ 中,$\begin{cases} \angle BGD = \angle DEB, \\ \angle GBD = \angle EDB, \\ BD = DB, \end{cases}$
$\therefore \triangle GBD\cong \triangle EDB(AAS)$,
$\therefore DE = BG$,
$\therefore DE + DF = BG + GH =$
对上述问题的结论,数学兴趣小组归纳出一个命题:等腰三角形底边上任意一点到两腰的距离之和为固定值,这个固定值是这个三角形腰上的
请根据他们的想法与思路,完成下列作图和填空:
(1)如图,在 $\triangle ABC$ 中,$AB = AC$,$D$ 是 $BC$ 边上一点,$DE\perp AB$ 于点 $E$. 用尺规过点 $D$ 作 $AC$ 的垂线交 $AC$ 于点 $F$ (不写作法,保留作图痕迹);
(2)已知:在 $\triangle ABC$ 中,$AB = AC$,$D$ 是 $BC$ 边上一点,$DE\perp AB$ 于点 $E$,$DF\perp AC$ 于点 $F$,求证:$DE + DF$ 为一固定值.
证明:过点 $B$ 作 $BH\perp AC$ 交 $CA$ 的延长线于点 $H$,过点 $D$ 作 $DG\perp BH$ 于点 $G$.
$\because DF\perp AC$,
$\therefore \angle DGH = \angle GHF = \angle DFH = 90^{\circ}$,
$\therefore$ 四边形 $DFHG$ 是
矩形
$\underline{①}$,$\therefore GH = DF$.
$\because DE\perp AB$,
$\therefore \angle BGD = \angle BED = 90^{\circ}$.
$\because AB = AC$,
$\therefore \angle ABC = \angle ACB$.
$\because \angle ACB + \angle GBD = 90^{\circ}$,$\angle ABC + \angle EDB = 90^{\circ}$,
∠GBD=∠EDB
$\therefore \underline{②}$.
在 $\triangle GBD$ 和 $\triangle EDB$ 中,$\begin{cases} \angle BGD = \angle DEB, \\ \angle GBD = \angle EDB, \\ BD = DB, \end{cases}$
$\therefore \triangle GBD\cong \triangle EDB(AAS)$,
$\therefore DE = BG$,
$\therefore DE + DF = BG + GH =$
BH
$\underline{③}$.对上述问题的结论,数学兴趣小组归纳出一个命题:等腰三角形底边上任意一点到两腰的距离之和为固定值,这个固定值是这个三角形腰上的
高
$\underline{④}$.
答案:
10. 解:
(1)尺规作图如解图①;

(2)根据题干信息作辅助线如解图②.

①矩形;②∠GBD=∠EDB;③BH;④高.
10. 解:
(1)尺规作图如解图①;

(2)根据题干信息作辅助线如解图②.

①矩形;②∠GBD=∠EDB;③BH;④高.
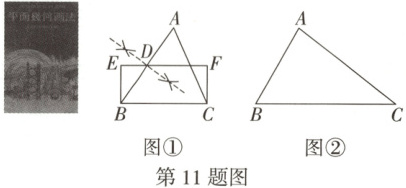
11. (2025 黑白卷)《平面几何画法》是朱铣和徐刚合编的一本平面几何教材,该书包含了大量的绘图示例和练习. 如图①,该书“例题 46”介绍了“画和定三角形等面积的矩形法”.
具体作法为:
①过 $B$ 点和 $C$ 点各作一条垂直于 $BC$ 的直线;
②作出 $AB$ 的中点 $D$,过点 $D$ 作平行于 $BC$ 的直线,与①中所得两条垂线交于 $E$,$F$ 两点,四边形 $BCFE$ 即为所求的矩形.
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图②中,作出与 $\triangle ABC$ 面积相等的矩形 $EBCF$ (保留作图痕迹,不写做法);
(2)请你证明(1)中的 $S_{\triangle ABC} = S_{矩形EBCF}$.
具体作法为:
①过 $B$ 点和 $C$ 点各作一条垂直于 $BC$ 的直线;
②作出 $AB$ 的中点 $D$,过点 $D$ 作平行于 $BC$ 的直线,与①中所得两条垂线交于 $E$,$F$ 两点,四边形 $BCFE$ 即为所求的矩形.
(1)请你依据以上步骤,用不带刻度的直尺和圆规在图②中,作出与 $\triangle ABC$ 面积相等的矩形 $EBCF$ (保留作图痕迹,不写做法);
(2)请你证明(1)中的 $S_{\triangle ABC} = S_{矩形EBCF}$.

答案:
1. (1)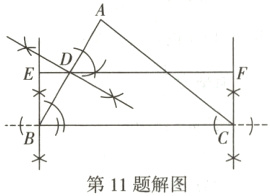
作图步骤:
①以$B$为圆心,适当长为半径画弧,交$BC$于两点,再分别以这两点为圆心,大于两点间距离一半的长为半径画弧,两弧相交于一点,过$B$与该点作直线$l_1\perp BC$;同理过$C$作直线$l_2\perp BC$。
②分别以$A$、$B$为圆心,大于$\frac{1}{2}AB$长为半径画弧,两弧分别相交,过两交点作直线,交$AB$于中点$D$。
③过$D$作直线$l// BC$,分别交$l_1$于$E$,交$l_2$于$F$,则矩形$EBCF$即为所求(作图痕迹略)。
2. (2)
证明:
解(证明):连接$CD$。
因为$D$是$AB$的中点,根据三角形中线的性质,三角形的中线将三角形分成面积相等的两部分,所以$S_{\triangle ADC}=S_{\triangle BDC}=\frac{1}{2}S_{\triangle ABC}$。
又因为$EF// BC$,$EB\perp BC$,$FC\perp BC$,所以四边形$EBCF$是矩形。
对于$\triangle BDC$和矩形$EBCF$,$\triangle BDC$与矩形$EBCF$等底($BC$为底),且$\triangle BDC$的高($D$到$BC$的距离)是矩形$EBCF$高($EB = FC$,$D$是$AB$中点,由平行线间的距离性质可知$D$到$BC$的距离等于$EB$(或$FC$)的一半)。
设$BC = a$,$EB = h$,$D$到$BC$的距离为$h_1$,则$h_1=\frac{1}{2}h$。
根据三角形面积公式$S_{\triangle}=\frac{1}{2}×底×高$,$S_{\triangle BDC}=\frac{1}{2}× BC× h_1$,矩形面积公式$S = 底×高$,$S_{矩形EBCF}=BC× h$。
把$h_1 = \frac{1}{2}h$代入$S_{\triangle BDC}=\frac{1}{2}× BC× h_1$得$S_{\triangle BDC}=\frac{1}{2}× BC×\frac{1}{2}h=\frac{1}{4}BC× h$,而$S_{矩形EBCF}=BC× h$,又因为$S_{\triangle ABC}=2S_{\triangle BDC}$。
$S_{\triangle ABC}=2×\frac{1}{2}× BC×\frac{1}{2}h$($S_{\triangle BDC}=\frac{1}{2}S_{\triangle ABC}$),$S_{矩形EBCF}=BC× h$,所以$S_{\triangle ABC}=S_{矩形EBCF}$。
综上,(1)按上述步骤作图;(2)证明如上。
1. (1)

作图步骤:
①以$B$为圆心,适当长为半径画弧,交$BC$于两点,再分别以这两点为圆心,大于两点间距离一半的长为半径画弧,两弧相交于一点,过$B$与该点作直线$l_1\perp BC$;同理过$C$作直线$l_2\perp BC$。
②分别以$A$、$B$为圆心,大于$\frac{1}{2}AB$长为半径画弧,两弧分别相交,过两交点作直线,交$AB$于中点$D$。
③过$D$作直线$l// BC$,分别交$l_1$于$E$,交$l_2$于$F$,则矩形$EBCF$即为所求(作图痕迹略)。
2. (2)
证明:
解(证明):连接$CD$。
因为$D$是$AB$的中点,根据三角形中线的性质,三角形的中线将三角形分成面积相等的两部分,所以$S_{\triangle ADC}=S_{\triangle BDC}=\frac{1}{2}S_{\triangle ABC}$。
又因为$EF// BC$,$EB\perp BC$,$FC\perp BC$,所以四边形$EBCF$是矩形。
对于$\triangle BDC$和矩形$EBCF$,$\triangle BDC$与矩形$EBCF$等底($BC$为底),且$\triangle BDC$的高($D$到$BC$的距离)是矩形$EBCF$高($EB = FC$,$D$是$AB$中点,由平行线间的距离性质可知$D$到$BC$的距离等于$EB$(或$FC$)的一半)。
设$BC = a$,$EB = h$,$D$到$BC$的距离为$h_1$,则$h_1=\frac{1}{2}h$。
根据三角形面积公式$S_{\triangle}=\frac{1}{2}×底×高$,$S_{\triangle BDC}=\frac{1}{2}× BC× h_1$,矩形面积公式$S = 底×高$,$S_{矩形EBCF}=BC× h$。
把$h_1 = \frac{1}{2}h$代入$S_{\triangle BDC}=\frac{1}{2}× BC× h_1$得$S_{\triangle BDC}=\frac{1}{2}× BC×\frac{1}{2}h=\frac{1}{4}BC× h$,而$S_{矩形EBCF}=BC× h$,又因为$S_{\triangle ABC}=2S_{\triangle BDC}$。
$S_{\triangle ABC}=2×\frac{1}{2}× BC×\frac{1}{2}h$($S_{\triangle BDC}=\frac{1}{2}S_{\triangle ABC}$),$S_{矩形EBCF}=BC× h$,所以$S_{\triangle ABC}=S_{矩形EBCF}$。
综上,(1)按上述步骤作图;(2)证明如上。
查看更多完整答案,请扫码查看


