《2026年万唯中考试题研究数学河北专版》

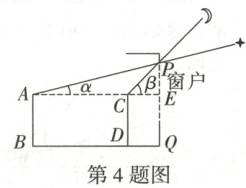
4. (2024河北22题)中国的探月工程激发了同学们对太空的兴趣. 某晚,淇淇在家透过窗户的最高点P恰好看到一颗星星,此时淇淇距窗户的水平距离BQ=4m,仰角为α;淇淇向前走了3m后到达点D,透过点P恰好看到月亮,仰角为β,如图是示意图. 已知,淇淇的眼睛与水平地面BQ的距离AB=CD=1.6m,点P到BQ的距离PQ=2.6m,AC的延长线交PQ于E. (注:图中所有点均在同一平面)
(1)求β的大小及$\tan α$的值;
(2)求CP的长及$\sin ∠APC$的值.

答案： $4.(1)β = 45^{\circ}, \tan \alpha = \frac{1}{4};$
$(2)CP = \sqrt{2} m,$
$\sin \angle APC = \frac{3\sqrt{34}}{34}.$

5. (2025样卷)风力发电是我国电力资源的重要组成部分. 嘉嘉为了解某风力发电机的风叶长度,通过测量其影子长度的方法进行计算. 如图(图中所有的点均在同一平面,太阳光线视为平行光线),线段OA,OB,OC表示三片风叶,$OA = OB = OC$,$∠AOB = ∠BOC = ∠COA = 120°$,某时刻OA,OB的影子恰好重合为线段EF,$OD ⊥ EF$于点D,测得DE=36m,EF=20m. 同一时刻测得高4m的标杆MN影长为3m.
(1)直接写出∠ABO的度数及OD的长;
(2)求风叶转动时点B到地面DF的最小距离.

答案： $5.(1)\angle ABO = 30^{\circ}, OD = 48 m;$
(2)风叶转动时点B到地面DF
的最小距离为16 m.

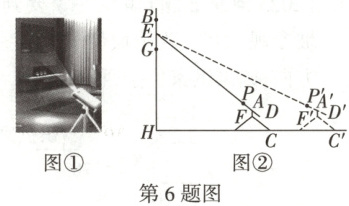
6. (2025黑白卷)图①是屏幕投影仪投屏情景图,图②是其侧面示意图,BG为投影高度,E为BG的中点,PE与投影仪PD在同一直线上,且与三角支架中的A-F-C在同一竖直平面内,$FC = 50$cm,$AF = 12$cm,$∠FCH = 37°$,且AF垂直于水平地面HC. (结果保留整数,参考数据:$\sin 37° ≈ 0.60$,$\cos 37° ≈ 0.80$,$\tan 37° ≈ 0.75$)
(1)求支架点F到水平地面HC的距离;
(2)若投影仪的尾端D与支架点F所在直线恰好平行于水平地面HC,测得$DF = 15$cm,$CH = 240$cm.
①求点E与水平地面HC之间的距离;
②若将投影仪水平后移1m,投影位置保持不变,此时投影仪的仰角为α($ED'$与水平地面HC的夹角),求$\tan α$的值.

答案： 6.
(1)支架点F到水平地面HC的
距离约为30 cm;
(2)①点E与水平地面HC之间
的距离约为202 cm;
$②\tan \alpha = \frac{8}{15}$