第46页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
例 新考法 跨物理学科 (2025保定模拟)某条东西方向道路双向共有三条车道,在早晚高峰经常会拥堵,某数学小组对该路段的交通量(辆/分钟)和时间进行了统计和分析,相应数据如下表所示,并发现交通量和时间的变化规律符合一次函数的特征,其中 $ y_2 = -x + 33 $。
(1)求 $ y_1 $ 与 $ x $ 的函数解析式;
(2)在13时:通过计算判断 $ y_1 $ 与 $ y_2 $ 的大小关系;
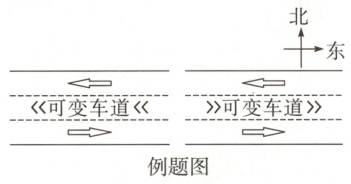
(3)如图,该小组希望设置“可变车道”来改善拥堵状况,根据交通量情况改变可变车道的行车方向. 单位时间内双向交通总量为 $ v = y_1 + y_2 $,交通量较大的为 $ y $,经查阅资料得:当 $ y \geq \frac{2}{3}v $ 时,是严重拥堵,需使可变车道行车方向与交通量较大的方向相同,以改善交通情况. 该路段从8时至20时,通过计算判断在严重拥堵时如何设置可变车道行车方向以缓解交通拥堵.

(1)求 $ y_1 $ 与 $ x $ 的函数解析式;
(2)在13时:通过计算判断 $ y_1 $ 与 $ y_2 $ 的大小关系;
(3)如图,该小组希望设置“可变车道”来改善拥堵状况,根据交通量情况改变可变车道的行车方向. 单位时间内双向交通总量为 $ v = y_1 + y_2 $,交通量较大的为 $ y $,经查阅资料得:当 $ y \geq \frac{2}{3}v $ 时,是严重拥堵,需使可变车道行车方向与交通量较大的方向相同,以改善交通情况. 该路段从8时至20时,通过计算判断在严重拥堵时如何设置可变车道行车方向以缓解交通拥堵.


答案:
1. (1)
解:设$y_1 = kx + b$($k\neq0$)。
把$(8,10)$,$(11,16)$代入$y_1 = kx + b$得:
$\begin{cases}8k + b = 10\\11k + b = 16\end{cases}$。
用$11k + b = 16$减去$8k + b = 10$得:
$(11k + b)-(8k + b)=16 - 10$。
$11k + b - 8k - b = 6$,即$3k = 6$,解得$k = 2$。
把$k = 2$代入$8k + b = 10$得:$8×2 + b = 10$,$16 + b = 10$,解得$b=-6$。
所以$y_1$与$x$的函数解析式为$y_1 = 2x-6$。
2. (2)
当$x = 13$时:
$y_1 = 2×13-6=20$,$y_2=-13 + 33 = 20$。
所以$y_1=y_2$。
3. (3)
因为$v=y_1 + y_2=(2x - 6)+(-x + 33)=x + 27$。
当$y_1\geq y_2$时,$2x-6\geq -x + 33$,$2x+x\geq33 + 6$,$3x\geq39$,解得$x\geq13$。
此时$y = y_1$,由$y\geq\frac{2}{3}v$得$2x-6\geq\frac{2}{3}(x + 27)$。
去括号得$2x-6\geq\frac{2}{3}x+18$。
移项得$2x-\frac{2}{3}x\geq18 + 6$。
合并同类项得$\frac{4}{3}x\geq24$,解得$x\geq18$。
当$y_1\lt y_2$时,$2x-6\lt -x + 33$,$2x+x\lt33 + 6$,$3x\lt39$,解得$x\lt13$。
此时$y = y_2$,由$y\geq\frac{2}{3}v$得$-x + 33\geq\frac{2}{3}(x + 27)$。
去括号得$-x + 33\geq\frac{2}{3}x+18$。
移项得$-x-\frac{2}{3}x\geq18 - 33$。
合并同类项得$-\frac{5}{3}x\geq - 15$,解得$x\leq9$。
所以当$8\leq x\leq9$时,$y_2\geq\frac{2}{3}v$,设置可变车道行车方向为自东向西;当$18\leq x\leq20$时,$y_1\geq\frac{2}{3}v$,设置可变车道行车方向为自西向东。
解:设$y_1 = kx + b$($k\neq0$)。
把$(8,10)$,$(11,16)$代入$y_1 = kx + b$得:
$\begin{cases}8k + b = 10\\11k + b = 16\end{cases}$。
用$11k + b = 16$减去$8k + b = 10$得:
$(11k + b)-(8k + b)=16 - 10$。
$11k + b - 8k - b = 6$,即$3k = 6$,解得$k = 2$。
把$k = 2$代入$8k + b = 10$得:$8×2 + b = 10$,$16 + b = 10$,解得$b=-6$。
所以$y_1$与$x$的函数解析式为$y_1 = 2x-6$。
2. (2)
当$x = 13$时:
$y_1 = 2×13-6=20$,$y_2=-13 + 33 = 20$。
所以$y_1=y_2$。
3. (3)
因为$v=y_1 + y_2=(2x - 6)+(-x + 33)=x + 27$。
当$y_1\geq y_2$时,$2x-6\geq -x + 33$,$2x+x\geq33 + 6$,$3x\geq39$,解得$x\geq13$。
此时$y = y_1$,由$y\geq\frac{2}{3}v$得$2x-6\geq\frac{2}{3}(x + 27)$。
去括号得$2x-6\geq\frac{2}{3}x+18$。
移项得$2x-\frac{2}{3}x\geq18 + 6$。
合并同类项得$\frac{4}{3}x\geq24$,解得$x\geq18$。
当$y_1\lt y_2$时,$2x-6\lt -x + 33$,$2x+x\lt33 + 6$,$3x\lt39$,解得$x\lt13$。
此时$y = y_2$,由$y\geq\frac{2}{3}v$得$-x + 33\geq\frac{2}{3}(x + 27)$。
去括号得$-x + 33\geq\frac{2}{3}x+18$。
移项得$-x-\frac{2}{3}x\geq18 - 33$。
合并同类项得$-\frac{5}{3}x\geq - 15$,解得$x\leq9$。
所以当$8\leq x\leq9$时,$y_2\geq\frac{2}{3}v$,设置可变车道行车方向为自东向西;当$18\leq x\leq20$时,$y_1\geq\frac{2}{3}v$,设置可变车道行车方向为自西向东。
查看更多完整答案,请扫码查看


