《2026年万唯中考试题研究数学河北专版》

$1. （2025$河北$22$题$）$一般固体都具有热胀冷缩的性质，固体受热后其长度的增加称为线膨胀$. $在$ （$本题涉及的温度均在此范围内$），$原长为$ l \, \mathrm { m } $的铜棒、铁棒受热后，伸长量$ y ( \mathrm { m } ) $与温度的增加量$ x ( ^ { \circ } \mathrm { C } ) $之间的关系均为$ y = \alpha l x ，$其中$ \alpha $为常数，称为该金属的线膨胀系数$. $已知铜的线膨胀系数$ \alpha _ { \mathrm { Cu } } = 1.7 × 10 ^ { - 5 } （$单位：$ / ^ { \circ } \mathrm { C } ）；$原长为$ 2.5 \, \mathrm { m } $的铁棒从$ $加热到$ $伸长了$ 1.8 × 10 ^ { - 3 } \, \mathrm { m } .$　　
$（1）$原长为$ 0.6 \, \mathrm { m } $的铜棒受热后升高$ ，$求该铜棒的伸长量$（$用科学记数法表示$）；$　　
$（2）$求铁的线膨胀系数$ \alpha _ { \mathrm { Fe } } ；$若原长为$ 1 \, \mathrm { m } $的铁棒受热后伸长$ 4.8 × 10 ^ { - 4 } \, \mathrm { m } ，$求该铁棒温度的增加量；　　
$（3）$将原长相等的铜棒和铁棒从$ $开始分别加热，当它们的伸长量相同时，若铁棒的温度比铜棒的高$ ，$求该铁棒温度的增加量$.$　　

答案：
(1)该铜棒的伸长量为$5.1 × 10^{-4} m$；
(2)铁的线膨胀系数$\alpha_{Fe} = 1.2 × 10^{-5}/^{\circ}C$，该铁棒温度的增加量为$40 ^{\circ}C$；
(3)该铁棒温度的增加量为$68 ^{\circ}C$。

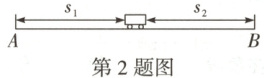
2. 新考法 跨物理学科 如图，在一条长为 $ 45 \, \mathrm { cm } $ 的水平直线轨道上，放置一辆长为 $ 5 \, \mathrm { cm } $ 的小车，开始时小车的左端与 $ A $ 处挡板重合，随后小车以 $ 4 \, \mathrm { cm } / \mathrm { s } $ 的速度匀速向右行驶，当小车与 $ B $ 处挡板碰撞后因为要改变方向需停顿 $ 1 \, \mathrm { s } $，随后以小于 $ 4 \, \mathrm { cm } / \mathrm { s } $ 的速度匀速返回，当小车的左端再次与 $ A $ 处挡板接触时停止运动. 在小车运动的过程中，设小车的左端与 $ A $ 处挡板的距离为 $ s _ { 1 } ( \mathrm { cm } ) $，右端与 $ B $ 处挡板之间的距离为 $ s _ { 2 } ( \mathrm { cm } ) $，小车出发后的时间为 $ t ( \mathrm { s } ) $，记 $ d = s _ { 1 } - s _ { 2 } $，小车从 $ A $ 处出发到最后返回 $ A $ 处，整个过程总用时 $ 27 \, \mathrm { s } $（含停顿时间）.
（1）求小车与 $ B $ 处挡板碰撞前，$ d $ 与 $ t $ 的函数解析式；
（2）求小车与 $ B $ 处挡板碰撞后，$ d $ 与 $ t $ 的函数解析式；
（3）当 $ d = 20 \, \mathrm { cm } $ 时，求小车运动的时间.

答案：
(1)$d$与$t$的函数解析式为$d = 8t - 40(0 \leq t ＜ 10)$；
(2)$d$与$t$的函数解析式为$d = \begin{cases} 40(10 ＜ t \leq 11), \\ -5t + 95(11 ＜ t \leq 27); \end{cases}$
(3)小车运动的时间为$7.5 s$或$15 s$。