《2025年新课堂同步学习与探究七年级数学上册人教版》

1. 在数轴上分别找出表示下列数的点.
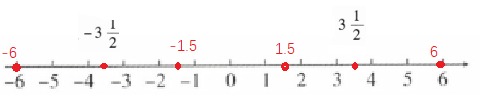
$6$与$-6$、$-3\frac{1}{2}$与$3\frac{1}{2}$、$-1.5$与$1.5$

答案：

2. 探究.
(1)上述各对数之间有什么相同点与不同点？
(2)它们在数轴上的位置有什么关系？

答案： 1. （1）
相同点：
每对数的绝对值相等，即$\vert6\vert = \vert - 6\vert=6$，$\vert - 3\frac{1}{2}\vert=\vert3\frac{1}{2}\vert = 3\frac{1}{2}$，$\vert - 1.5\vert=\vert1.5\vert = 1.5$。
不同点：
每对数的符号不同，一正一负。
2. （2）
解：
在数轴上，$6$与$-6$、$-3\frac{1}{2}$与$3\frac{1}{2}$、$-1.5$与$1.5$都关于原点对称。因为数轴上原点左边的数为负数，右边的数为正数，且互为相反数的两个数（$a$与$-a$）到原点的距离$\vert a\vert=\vert - a\vert$，所以它们分别位于原点两侧，且到原点的距离相等。

3. 像$6$和$-6$、$5$和$-5$这样，只有符号不同的两个数叫作互为相反数.

答案： 3.只有符号不同

4. 在数轴上，位于原点两旁、并且到原点的距离相等的两个点表示的两个数互为相反数.

答案： 4.相等 相反数

5. 在数轴上，互为相反数的两个数表示的点关于原点对称.

答案： 5.对称

6. 你是怎样理解相反数定义中“只有”和“互为”的含义的？

答案： 6.“只有”表示除了符号不同,其他都相同;“互为”表示相反数应该成对出现.

7. $-(+5)$表示$+5$的相反数，$+5$的相反数是-5，所以$-(+5)=$-5；$-(-5)$表示-5的相反数，$-5$的相反数是5，所以$-(-5)=$5.
总结：在正数前面添上“$-$”号，就得到正数的相反数；在任意一个数前面添上“$-$”号后，新的数表示原数的相反数.

答案： 7.-5 -5 -5 5 5

8. 化简：$-(+0.5)=$___，$-(-28)=$___；$-(-0.5)=$____，$-(+2.8)=$____.

答案： 8.-0.5 28 0.5 -2.8

【例$1$】指出一列数$-2.4$，$1.7$，$1$，$-0.6$的相反数.
【例$2$】化简下列数.
(1)$-(+0.25)$ (2)$-(+5)$
(3)$-(-a)$ (4)$-[-(+1)]$

答案： 【例1】-2.4,1.7,1,-0.6的相反数分别是2.4,
-1.7,-1,0.6.
【例2】解
(1)-(+0.25)= -0.25.
(2)-(+5)= -5.
(3)-(-a)=a.
(4)-[-(+1)]=1.

变式：(1)如果$-a=-9$，那么$-a$的相反数是9.
(2)若$-x=7$，则$x=$-7；若$x=4$，则$-x=$-4.
(3)若$-(a-5)$是负数，则$a-5$＞$0$.

答案： 变式:
(1)9
(2)-7 -4
(3)＞

1. 判断.
(1)$-5$是$5$的相反数. (√)
(2)$-5$是相反数. (×)
(3)$-5$和$5$互为相反数. (√)
(4)相反数等于它本身的数只有$0$. (√)

答案： 1.
(1)√
(2)×
(3)√
(4)√

2. $-2$的相反数是(B).

A.$-2$
B.$2$
C.$-\frac{1}{2}$
D.$\frac{1}{2}$

答案： 2.B

3. $\frac{1}{3}$的相反数是(D).

A.$3$
B.$-3$
C.$\frac{1}{3}$
D.$-\frac{1}{3}$

答案： 3.D

4. 下列说法正确的是(B).

A.$\frac{2}{3}$和$\frac{3}{2}$互为相反数
B.$\frac{1}{8}$和$-0.125$互为相反数
C.$-a$的相反数是正数
D.两个表示相反意义的数是相反数

答案： 4.B