《2025年新课堂同步学习与探究七年级数学上册人教版》

【例 2】求 $ \frac{1}{2}-2x-\frac{1}{3}y^{2}+(-\frac{3}{2}x+\frac{1}{3}y^{2}) $ 的值,其中 $ x = - 2,y=\frac{2}{3} $.
注意:求整式的值,一般先化简再求值,只有当题目中含未知数的部分可以看成一个整体时,才可用整体代入法,这样会使运算简便.

答案： $\frac{15}{2}$

【例 3】笔记本的单价是 $ x $ 元,圆珠笔的单价是 $ y $ 元. 小红买 3 本笔记本、2 支圆珠笔,小明买 4 本笔记本、3 支圆珠笔. 小红和小明买这些笔记本和圆珠笔一共花费多少钱?
注意:按代数式的书写规则,代数式后面有单位,要将代数式作为整体加括号. 对于同一问题情景,从不同的角度考虑问题可以列出不同的式子,但最终得到同一结果.

答案： 小红花费：$(3x + 2y)$元
小明花费：$(4x + 3y)$元
一共花费：$(3x + 2y) + (4x + 3y) = 7x + 5y$元
答：一共花费$(7x + 5y)$元。

【例 4】做大、小两个长方体纸盒,尺寸如下(单位:厘米):

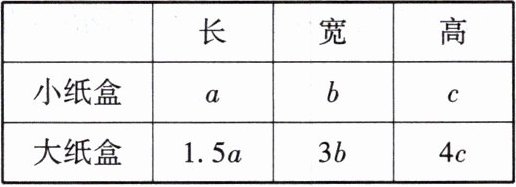
(1)做这两个纸盒共用料多少平方厘米?
(2)做 1 个大纸盒比做 1 个小纸盒多用料多少平方厘米?

答案：
(1)小纸盒表面积：$2(ab + bc + ac)$平方厘米，大纸盒表面积：$2(1.5a×3b + 3b×4c + 1.5a×4c) = 2(4.5ab + 12bc + 6ac) = 9ab + 24bc + 12ac$平方厘米，共用料：$2(ab + bc + ac) + 9ab + 24bc + 12ac = 2ab + 2bc + 2ac + 9ab + 24bc + 12ac = 11ab + 26bc + 14ac$平方厘米。
(2)多用料：$(9ab + 24bc + 12ac) - 2(ab + bc + ac) = 9ab + 24bc + 12ac - 2ab - 2bc - 2ac = 7ab + 22bc + 10ac$平方厘米。
(1) $11ab + 26bc + 14ac$；
(2) $7ab + 22bc + 10ac$

1. 式子 $ 3a^{2}-b^{2} $ 与 $ a^{2}+b^{2} $ 的差是(B).

A.$ 2a^{2} $
B.$ 2a^{2}-2b^{2} $
C.$ 4a^{2} $
D.$ 4a^{2}-2b^{2} $

答案： 1. B

2. $ -a + b - c $ 的相反数是(B).

A.$ -a - b + c $
B.$ a - b + c $
C.$ -a - b + c $
D.$ -a - b - c $

答案： 2. B

3. 若 $ (a^{2}-3a - 1)+A=a^{2}-a + 4 $,则 $ A = $2a + 5.

答案： 3. 2a + 5

4. 个位数字是 $ a $、十位数字是 $ b $、百位数字是 $ c $ 的三位数与把该三位数的个位数字与百位数字对调位置后所得的三位数的差为99c - 99a.

答案： 4. 99c - 99a