《2025年新课堂同步学习与探究七年级数学上册人教版》

1. 已知$n$是整数，在①$2n + 3$，②$2n - 1$中，能表示“任意奇数”的(C).

A.只有①
B.只有②
C.两个都可以
D.一个也没有

答案： 1.C

2. 某比赛今年有$a$部作品参赛，比去年增加了$40\%$还多$2$部，设去年参赛的作品有$b$部，则$b$是(A).

A.$\frac{a - 2}{1 + 40\%}$
B.$\frac{a + 2}{1 + 40\%}$
C.$a(1 + 40\%) + 2$
D.$a(1 + 40\%) - 2$

答案： 2.A

3. 某市市区人口为$a$万，市区绿化面积为$m$万平方米，则平均每个人拥有绿地\frac{m}{a}平方米.

答案： $3.\frac{m}{a}$

4. 某城市$5$年前人均年收入为$n$元，预计今年人均年收入比$5$年前的$2$倍多$500$元，那么今年该市人均年收入将达(2n+500)元.

答案： 4.(2n+500)

5. 已知长方形的周长是$m$厘米，一边长为$a$厘米，则这个长方形的面积是(\frac{m}{2}-a)a平方厘米.

答案： $5.(\frac{m}{2}-a)a$

6. 甲、乙两人分别从$A$，$B$两地同时出发，相向而行. 甲的速度为$a$千米/时，乙的速度为$b$千米/时，经过$2$小时两人相遇，那么$A$，$B$两地的距离是(2a+2b)千米.

答案： 6.(2a+2b)

7. 一组数为$2$，$4$，$6$，$a$，$10$，$12$，$14$，$b$，$18$，…，则$a =$8，$b =$16，第$n$个数为2n.

答案： 7.8 16 2n

1. 用代数式表示“体积为$V$、高为$h$的长方体的底面积”为\frac{V}{h}.

答案： $1.\frac{V}{h}$

2. 设银行一年定期存款的利率为$1.5\%$，存入$m$元，一年到期的利息为1.5\%m元.

答案： 2.1.5\%m

3. 两船从同一港口同时出发反向而行，甲船顺水航行，乙船逆水航行，两船在静水中前进的速度为$40$千米/时，水流的速度为$a$千米/时，则$2.5$小时后甲船比乙船多航行5a千米.

答案： 3.5a

4. 语句“$a$的平方与$b$的平方的和”用含$a$，$b$的代数式表示为a^{2}+b^{2}.

答案： $4.a^{2}+b^{2}$

5. $3$支球队进行单循环比赛，总场次为3，$n$支球队为\frac{n(n - 1)}{2}.

答案： $5.3\frac{n(n - 1)}{2}$

6. 我们知道：$23 = 2×10 + 3$，$865 = 8×100 + 6×10 + 5$.
类似地，$5984 =$5×1000+9×100+8×10+4.
若一个三位数的个位数字为$a$，十位数字为$b$，百位数字为$c$，则此三位数可表示为1000c+100b+a.

答案： 6.5×1000+9×100+8×10+4 1000c+100b+a

7. 用黑、白两种颜色的正六边形地面砖按如下所示的规律拼成若干个图案：

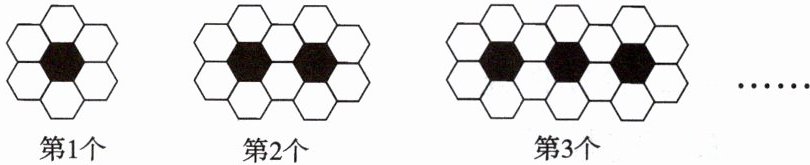
(1)第$4$个图案中白色的地面砖有18块；
(2)第$n$个图案中白色的地面砖有4n+2块.

答案： 7.
(1)18
(2)4n+2

8. 阅读下面的材料，并回答问题：
你能比较两个数$2023^{2024}$与$2024^{2023}$的大小吗？
为了解决这个问题，先将问题一般化，即比较$n^{n + 1}$和$(n + 1)^n$的大小($n\geq1$且$n$为整数)，然后从分析$n = 1$，$2$，$3$，$4$，$5$，…这些简单情况入手，从中发现规律，经过归纳，猜想出结论(在横线上填“$＞$”“$＜$”或“$=$”).
(1)通过计算比较大小：
①$1^2$＜$2^1$；
②$2^3$＜$3^2$；
③$3^4$＜$4^3$；
④$4^5$＜$5^4$；
⑤$5^6$＜$6^5$.
(2)经过归纳，可以猜想出$n^{n + 1}$和$(n + 1)^n$的大小关系是$n^{n + 1}$＜$(n + 1)^n$.
(3)根据上面的归纳猜想，可以得到$2023^{2024}$＜$2024^{2023}$.

答案： 8.
(1)①＜ ②＜ ③＜ ④＜ ⑤＜
(2)＜
(3)＜