第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
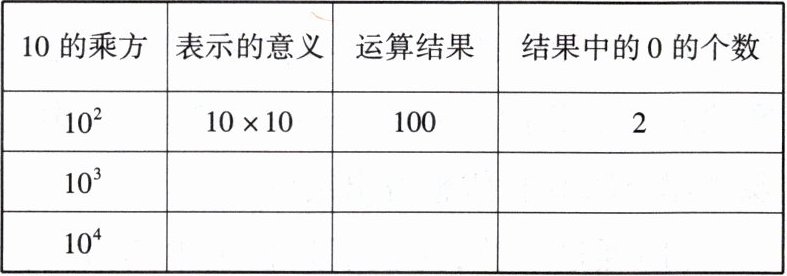
1. 根据乘方的意义填写下表:

答案:
| $10$ 的乘方 | 表示的意义 | 运算结果 | 结果中的 0 的个数 |
| --- | --- | --- | --- |
| $10^2$ | $10 × 10$ | $100$ | $2$ |
| $10^3$ | $10 × 10 × 10$ | $1000$ | $3$ |
| $10^4$ | $10 × 10 × 10 × 10$ | $10000$ | $4$ |
| --- | --- | --- | --- |
| $10^2$ | $10 × 10$ | $100$ | $2$ |
| $10^3$ | $10 × 10 × 10$ | $1000$ | $3$ |
| $10^4$ | $10 × 10 × 10 × 10$ | $10000$ | $4$ |
2. (1)2008 年北京奥运会主会场——鸟巢,能容纳 91 000 位观众.
(2)世界总人口数约为 6 100 000 000 人.
根据预习尝试把 91 000 和 6 100 000 000 写成 $ a × 10^{n} $ (其中 $ 1 \leq a \lt 10 $, $ n $ 是正整数)的形式.
(2)世界总人口数约为 6 100 000 000 人.
根据预习尝试把 91 000 和 6 100 000 000 写成 $ a × 10^{n} $ (其中 $ 1 \leq a \lt 10 $, $ n $ 是正整数)的形式.
答案:
(1) 对于 $91000$:
$a$ 是 $9.1$(将 $91000$ 转换为 $1 \leq a \lt 10$ 的形式);
$n$ 是 $4$(因为需要将小数点从 $9.1$ 移动到 $91000$ 的最后一位,移动了 $4$ 位)。
所以,$91000 = 9.1 × 10^{4}$。
(2) 对于 $6100000000$:
$a$ 是 $6.1$(将 $6100000000$ 转换为 $1 \leq a \lt 10$ 的形式);
$n$ 是 $9$(因为需要将小数点从 $6.1$ 移动到 $6100000000$ 的最后一位,移动了 $9$ 位)。
所以,$6100000000 = 6.1 × 10^{9}$。
(1) 对于 $91000$:
$a$ 是 $9.1$(将 $91000$ 转换为 $1 \leq a \lt 10$ 的形式);
$n$ 是 $4$(因为需要将小数点从 $9.1$ 移动到 $91000$ 的最后一位,移动了 $4$ 位)。
所以,$91000 = 9.1 × 10^{4}$。
(2) 对于 $6100000000$:
$a$ 是 $6.1$(将 $6100000000$ 转换为 $1 \leq a \lt 10$ 的形式);
$n$ 是 $9$(因为需要将小数点从 $6.1$ 移动到 $6100000000$ 的最后一位,移动了 $9$ 位)。
所以,$6100000000 = 6.1 × 10^{9}$。
1. $ 10^{n} $ 的特征.
计算并观察:
$ 10^{1} = 10 $, $ 10^{2} = 100 $, $ 10^{3} = 1000 $,
$ 10^{4} = 10 000 $, $\cdots$, $ 10^{10} = 10 000 000 000 $.
提问: $ 10^{n} $ 中的 $ n $ 表示 $ n $ 个 10 相乘,它与运算结果中 0 的个数有什么关系?与运算结果的数位有什么关系?
(1) $ 10^{n} = 1\underbrace{00\cdots 0}_{n 个 0} $, $ n $ 恰巧是 1 后面 0 的个数;
(2) $ 10^{n} = \underbrace{100\cdots 0}_{(n + 1)位} $,比运算结果的位数少 1.
反之,1 后面有多少个 0,10 的幂指数就是多少,如 $\underbrace{10 000 000}_{7 个 0} = 10^{7} $.
计算并观察:
$ 10^{1} = 10 $, $ 10^{2} = 100 $, $ 10^{3} = 1000 $,
$ 10^{4} = 10 000 $, $\cdots$, $ 10^{10} = 10 000 000 000 $.
提问: $ 10^{n} $ 中的 $ n $ 表示 $ n $ 个 10 相乘,它与运算结果中 0 的个数有什么关系?与运算结果的数位有什么关系?
(1) $ 10^{n} = 1\underbrace{00\cdots 0}_{n 个 0} $, $ n $ 恰巧是 1 后面 0 的个数;
(2) $ 10^{n} = \underbrace{100\cdots 0}_{(n + 1)位} $,比运算结果的位数少 1.
反之,1 后面有多少个 0,10 的幂指数就是多少,如 $\underbrace{10 000 000}_{7 个 0} = 10^{7} $.
答案:
(1)(题目已给出答案形式)$n$ 恰巧是 1 后面 0 的个数;
(2)(题目已给出答案形式)比运算结果的位数少 1。
(1)(题目已给出答案形式)$n$ 恰巧是 1 后面 0 的个数;
(2)(题目已给出答案形式)比运算结果的位数少 1。
2. 练习.
(1)把下列数写成 10 的幂的形式:1 000,100 000 000,100 000 000 000.
(2)指出下列数是几位数: $ 10^{3} $, $ 10^{5} $, $ 10^{12} $, $ 10^{100} $.
(1)把下列数写成 10 的幂的形式:1 000,100 000 000,100 000 000 000.
(2)指出下列数是几位数: $ 10^{3} $, $ 10^{5} $, $ 10^{12} $, $ 10^{100} $.
答案:
(1)
$1000 = 10^{3}$;
$100000000 = 10^{8}$;
$100000000000 = 10^{11}$;
(2)
$10^{3}$是4位数(因为$10^{3}=1000$);
$10^{5}$是6位数(因为$10^{5}=100000$);
$10^{12}$是13位数;
$10^{100}$是101位数。
(1)
$1000 = 10^{3}$;
$100000000 = 10^{8}$;
$100000000000 = 10^{11}$;
(2)
$10^{3}$是4位数(因为$10^{3}=1000$);
$10^{5}$是6位数(因为$10^{5}=100000$);
$10^{12}$是13位数;
$10^{100}$是101位数。
3. 探究:基于 $ 10^{n} $ 的特征填空.
$ 2 800 000 000 = 2.8 × 10^{( )} $,
$ 12 300 000 000 = $$ × 10^{10} $,
$ 500 000 000 = $$ × 10^{8} $,
$ 46 000 000 = 4.6 × 10^{( )} $,
$ 10 300 000 000 = 1.03 × 10^{( )} $,
$ 41 000 000 = $$ × 10^{7} $.
总结:(1)任何一个数都可以表示成整数数位是一位数的数乘以 10 的 $ n $ 次幂的形式.
例如:
$ 100 = 1 × 100 = 1 × 10^{2} $,
$ 6 000 = 6 × 1 000 = 6 × 10^{3} $,
$ 7 500 = 7.5 × 1 000 = 7.5 × 10^{3} $.
(2)科学记数法的定义:
根据上面的例子,我们把大于 10 的数记成 $ a × 10^{n} $ 的形式,其中 $ a $ 是整数数位只有一位的数, $ n $ 是自然数,这种记数法叫作科学记数法. 现在,我们只学习绝对值大于 10 的数的科学记数法,以后我们还要学习其他一些数的科学记数法. 说它科学,因为它简单明了,易读、易记、易判断大小,在自然科学中经常用到.
$ 2 800 000 000 = 2.8 × 10^{( )} $,
$ 12 300 000 000 = $$ × 10^{10} $,
$ 500 000 000 = $$ × 10^{8} $,
$ 46 000 000 = 4.6 × 10^{( )} $,
$ 10 300 000 000 = 1.03 × 10^{( )} $,
$ 41 000 000 = $$ × 10^{7} $.
总结:(1)任何一个数都可以表示成整数数位是一位数的数乘以 10 的 $ n $ 次幂的形式.
例如:
$ 100 = 1 × 100 = 1 × 10^{2} $,
$ 6 000 = 6 × 1 000 = 6 × 10^{3} $,
$ 7 500 = 7.5 × 1 000 = 7.5 × 10^{3} $.
(2)科学记数法的定义:
根据上面的例子,我们把大于 10 的数记成 $ a × 10^{n} $ 的形式,其中 $ a $ 是整数数位只有一位的数, $ n $ 是自然数,这种记数法叫作科学记数法. 现在,我们只学习绝对值大于 10 的数的科学记数法,以后我们还要学习其他一些数的科学记数法. 说它科学,因为它简单明了,易读、易记、易判断大小,在自然科学中经常用到.
答案:
9;1.23;5;7;10;4.1
查看更多完整答案,请扫码查看


