第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
阅读教材第38—40页的内容,然后回答问题.
1. 计算下列乘法算式:
(1)$3×3=$,$3×2=$,$3×1=$,$3×0=$.
(2)$3×(-1)=$,$3×(-2)=$,$3×(-3)=$.
观察后发现规律:随着后一乘数逐次递减1,积逐次递减.
2. 计算下列乘法算式:
(1)$3×3=$,$2×3=$,$1×3=$,$0×3=$.
(2)$(-1)×3=$,$(-2)×3=$,$(-3)×3=$.
观察后发现规律:随着前一乘数逐次递减1,积逐次递减.
3. 有关有理数的乘法运算要从符号和绝对值这两个角度去观察.我们发现:
从符号上来说:正数乘正数,积为;正数乘负数,积为;负数乘正数,积为.
从绝对值上来说:积的绝对值等于各乘数的积.
所以,我们在进行有理数的乘法运算时,既要考虑符号,又要考虑大小.
4. 计算下列乘法算式:
$(-3)×3=$,
$(-3)×2=$,
$(-3)×1=$,
$(-3)×0=$,
$(-3)×(-1)=$,
$(-3)×(-2)=$,
$(-3)×(-3)=$.
我们发现:负数乘正数,积为;负数乘负数,积为;积的绝对值等于各乘数.
$(+2)×(+3)=+6$ ①
$(-2)×(+3)=-6$ ②
$(+2)×(-3)=-6$ ③
$(-2)×(-3)=+6$ ④
比较①②③④,你有什么发现?
总结:有理数的乘法法则如下:
两数相乘,同号得,异号得,并把绝对值. 任何数同0相乘,都得.
1. 计算下列乘法算式:
(1)$3×3=$,$3×2=$,$3×1=$,$3×0=$.
(2)$3×(-1)=$,$3×(-2)=$,$3×(-3)=$.
观察后发现规律:随着后一乘数逐次递减1,积逐次递减.
2. 计算下列乘法算式:
(1)$3×3=$,$2×3=$,$1×3=$,$0×3=$.
(2)$(-1)×3=$,$(-2)×3=$,$(-3)×3=$.
观察后发现规律:随着前一乘数逐次递减1,积逐次递减.
3. 有关有理数的乘法运算要从符号和绝对值这两个角度去观察.我们发现:
从符号上来说:正数乘正数,积为;正数乘负数,积为;负数乘正数,积为.
从绝对值上来说:积的绝对值等于各乘数的积.
所以,我们在进行有理数的乘法运算时,既要考虑符号,又要考虑大小.
4. 计算下列乘法算式:
$(-3)×3=$,
$(-3)×2=$,
$(-3)×1=$,
$(-3)×0=$,
$(-3)×(-1)=$,
$(-3)×(-2)=$,
$(-3)×(-3)=$.
我们发现:负数乘正数,积为;负数乘负数,积为;积的绝对值等于各乘数.
$(+2)×(+3)=+6$ ①
$(-2)×(+3)=-6$ ②
$(+2)×(-3)=-6$ ③
$(-2)×(-3)=+6$ ④
比较①②③④,你有什么发现?
总结:有理数的乘法法则如下:
两数相乘,同号得,异号得,并把绝对值. 任何数同0相乘,都得.
答案:
1.
(1)9;6;3;0
(2)-3;-6;-9;3
2.
(1)9;6;3;0
(2)-3;-6;-9;3
3. 正数;负数;负数;绝对值
4. -9;-6;-3;0;3;6;9;负数;正数;绝对值的积;正;负;相乘;0
(1)9;6;3;0
(2)-3;-6;-9;3
2.
(1)9;6;3;0
(2)-3;-6;-9;3
3. 正数;负数;负数;绝对值
4. -9;-6;-3;0;3;6;9;负数;正数;绝对值的积;正;负;相乘;0
【例1】计算.
(1)$(-3)×9$
(2)$8×1$
(3)$8×(-1)$
(4)$\left(-\dfrac{1}{2}\right)×(-2)$
总结:一个数同1相乘,结果是,一个数同-1相乘,得原数的.
(1)$(-3)×9$
(2)$8×1$
(3)$8×(-1)$
(4)$\left(-\dfrac{1}{2}\right)×(-2)$
总结:一个数同1相乘,结果是,一个数同-1相乘,得原数的.
答案:
(1)
$(-3)×9 = - (3 × 9)=-27$
(2)
$8×1 = 8$
(3)
$8×(-1)=- (8×1)= - 8$
(4)
$\left(-\dfrac{1}{2}\right)×(-2)=+\left(\dfrac{1}{2}×2\right)=1$
总结:一个数同$1$相乘,结果是它本身,一个数同$-1$相乘,得原数的相反数。
故答案为:它本身;相反数。
(1)
$(-3)×9 = - (3 × 9)=-27$
(2)
$8×1 = 8$
(3)
$8×(-1)=- (8×1)= - 8$
(4)
$\left(-\dfrac{1}{2}\right)×(-2)=+\left(\dfrac{1}{2}×2\right)=1$
总结:一个数同$1$相乘,结果是它本身,一个数同$-1$相乘,得原数的相反数。
故答案为:它本身;相反数。
【例2】填写下表:
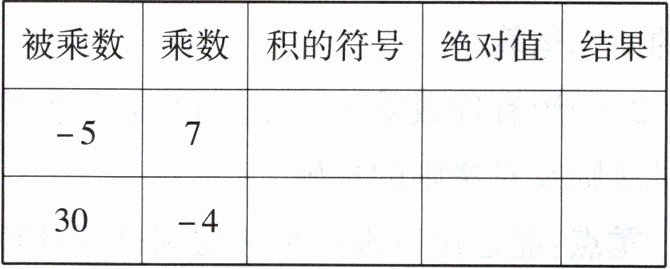
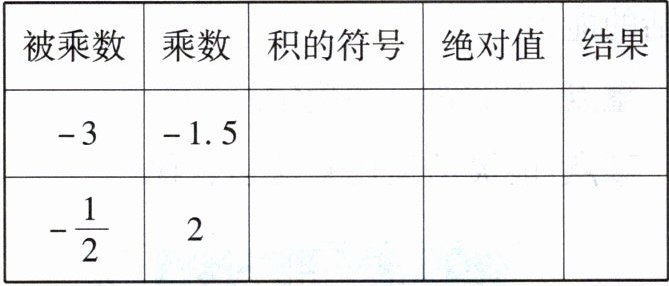
总结:两数相乘,一看两数是同号还是;二确定的符号;三再把相乘. 简称“一看二定三计算”.


总结:两数相乘,一看两数是同号还是;二确定的符号;三再把相乘. 简称“一看二定三计算”.
答案:
被乘数为$-5$,乘数为$7$:
积的符号:负号(因为异号相乘为负)。
绝对值:$| -5 | × | 7 | = 5 × 7 = 35$。
结果:$-35$。
被乘数为$30$,乘数为$-4$:
积的符号:负号(因为异号相乘为负)。
绝对值:$| 30 | × | -4 | = 30 × 4 = 120$。
结果:$-120$。
被乘数为$-3$,乘数为$-1.5$:
积的符号:正号(因为同号相乘为正)。
绝对值:$| -3 | × | -1.5 | = 3 × 1.5 = 4.5$。
结果:$4.5$。
被乘数为$-\frac{1}{2}$,乘数为$2$:
积的符号:负号(因为异号相乘为负)。
绝对值:$\left| -\frac{1}{2} \right| × | 2 | = \frac{1}{2} × 2 = 1$。
结果:$-1$。
总结:两数相乘,一看两数是同号还是异号;二确定积的符号;三再把绝对值相乘,简称“一看二定三计算”。
填表如下:
| 被乘数 | 乘数 | 积的符号 | 绝对值 | 结果 |
| --- | --- | --- | --- | --- |
| $-5$ | $7$ | 负 | $35$ | $-35$ |
| $30$ | $-4$ | 负 | $120$ | $-120$ |
| $-3$ | $-1.5$ | 正 | $4.5$ | $4.5$ |
| $-\frac{1}{2}$ | $2$ | 负 | $1$ | $-1$ |
总结填表:
异号;积;绝对值。
积的符号:负号(因为异号相乘为负)。
绝对值:$| -5 | × | 7 | = 5 × 7 = 35$。
结果:$-35$。
被乘数为$30$,乘数为$-4$:
积的符号:负号(因为异号相乘为负)。
绝对值:$| 30 | × | -4 | = 30 × 4 = 120$。
结果:$-120$。
被乘数为$-3$,乘数为$-1.5$:
积的符号:正号(因为同号相乘为正)。
绝对值:$| -3 | × | -1.5 | = 3 × 1.5 = 4.5$。
结果:$4.5$。
被乘数为$-\frac{1}{2}$,乘数为$2$:
积的符号:负号(因为异号相乘为负)。
绝对值:$\left| -\frac{1}{2} \right| × | 2 | = \frac{1}{2} × 2 = 1$。
结果:$-1$。
总结:两数相乘,一看两数是同号还是异号;二确定积的符号;三再把绝对值相乘,简称“一看二定三计算”。
填表如下:
| 被乘数 | 乘数 | 积的符号 | 绝对值 | 结果 |
| --- | --- | --- | --- | --- |
| $-5$ | $7$ | 负 | $35$ | $-35$ |
| $30$ | $-4$ | 负 | $120$ | $-120$ |
| $-3$ | $-1.5$ | 正 | $4.5$ | $4.5$ |
| $-\frac{1}{2}$ | $2$ | 负 | $1$ | $-1$ |
总结填表:
异号;积;绝对值。
查看更多完整答案,请扫码查看


