《2025年新课堂同步学习与探究七年级数学上册人教版》

13. 一个三位数的个位上的数字是$a$，十位上的数字是个位上数字的平方，百位上的数字是个位上数字的立方，则这个三位数是100a^{3}+10a^{2}+a。

答案： $13. 100a^{3}+10a^{2}+a$

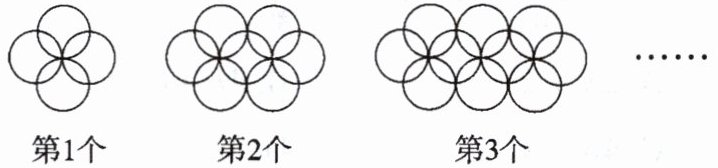
14. 一组有规律的图案如图所示，它们由半径相同的圆形组成，依此规律，第$n$个图案中有(3n + 1)个圆形(用含有$n$的代数式表示)。

……

答案： 14. (3n + 1)

15. 一组按一定规律排列的式子为$a^2$，$\dfrac{a^5}{2}$，$\dfrac{a^8}{3}$，$\dfrac{a^{11}}{4}$，…，则第$n$个式子是\frac{a^{3n - 1}}{n} ($a \neq 0$，$n$为正整数)。

答案： $15. \frac{a^{3n - 1}}{n}$

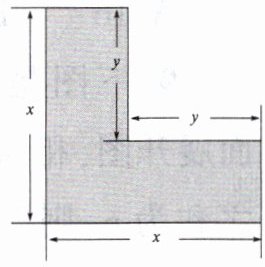
16. 已知如图所示。
(1)请用含$x$和$y$的代数式表示阴影部分的面积。
(2)当$x = 4$，$y = 3$时，阴影部分的面积是多少？

答案： $16. (1)x^{2}-y^{2} (2)7$

17. 观察下列几个等式：
$1 + 2 + 1 = 2^2 = 4$，
$1 + 2 + 3 + 2 + 1 = 3^2 = 9$，
$1 + 2 + 3 + 4 + 3 + 2 + 1 = 4^2 = 16$。
聪明的你一定能找出其中的规律，请利用该规律填空：
$1 + 2 + 3 + \cdots + 99 + 100 + 99 + \cdots + 3 + 2 + 1 =$100^{2}$=$10000。
由此，我们可利用上式得到求若干个连续自然数和的方法，思考后解答问题：
(1)求$1 + 2 + 3 + \cdots + 99 + 100$的值；
(2)由此可得$1 + 2 + 3 + \cdots + n =$\frac{n(n + 1)}{2}。

答案： $17. 100^{2}=10000 (1)5050 (2)\frac{n(n + 1)}{2}$

18. (1)当$a = -5$，$b = -6$，$c = 7$时，求$a^2 - bc - ac$的值。
(2)已知$a$，$b$互为相反数，$c$，$d$互为倒数，$m$的绝对值是$2$，求$\dfrac{|a + b|}{2m^2 + 1} + 4m - 3cd$的值。

答案： 18.
(1)102
(2)5或 - 11

19. 云南成为全国首个“吃螃蟹”的省份，将中考体育从$50$分提升到$100$分。某校为适应新的中考要求，决定在网上订购一批某品牌的排球和跳绳，每个排球定价为$140$元，每条跳绳定价为$30$元。现有$A$，$B$两家网店均提供包邮服务，并提出了各自的优惠方案。$A$网店：买$1$个排球送$1$条跳绳；$B$网店：排球和跳绳都按定价的$9$折销售。已知该校要购买$60$个排球、$a$条跳绳$(a ＞ 60)$。
(1)若在$A$网店购买，需付款(6600 + 30a)元(用含$a$的代数式表示)；若在$B$网店购买，需付款(7560 + 27a)元(用含$a$的代数式表示)。
(2)若$a = 100$，通过计算比较在哪家网店购买省钱。
(3)当$a = 100$时，你能给出一种更为省钱的购买方案吗？试写出你的购买方法，并计算需付款多少元。

答案： 19.
(1)(6600 + 30a) (7560 + 27a)
(2)A网店
(3)先在A网店购买60个排球、60条跳绳，再在B网店购买40条跳绳，付款9480元.