第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
3. 一个多项式含有几项,就叫几项式. 多项式里次数最高项的次数,就是这个多项式的次数. 例如:多项式$3x^{2} - 2x + 5$是一个二次三项式.
答案:
答题卡填入内容如下:
该题目为定义说明题,无需计算,答案(结论)为:
多项式项数:多项式中包含的单项式个数即为几项式;
多项式次数:多项式中次数最高的单项式的次数即为该多项式的次数;
举例:多项式 $3x^{2} - 2x + 5$ 是一个二次三项式。
该题目为定义说明题,无需计算,答案(结论)为:
多项式项数:多项式中包含的单项式个数即为几项式;
多项式次数:多项式中次数最高的单项式的次数即为该多项式的次数;
举例:多项式 $3x^{2} - 2x + 5$ 是一个二次三项式。
4. 单项式与多项式统称为整式.
答案:
4. 整式的定义:单项式与多项式统称为整式。
【例1】下列整式中,哪些是单项式?哪些是多项式?是单项式的指出系数和次数,是多项式的指出项和次数.
$- \frac {1}{2}a^{b},\frac {m^{4}n^{2}}{7},x^{2} + y^{2} - 1,x,32t^{3},\frac {π}{3},3x^{2} - y + 3xy^{3} + x^{4} - 1,2x - y$
注意:(1)多项式的各项应包括它们前面的符号;(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;(4)一个多项式的最高次项可以不唯一.
$- \frac {1}{2}a^{b},\frac {m^{4}n^{2}}{7},x^{2} + y^{2} - 1,x,32t^{3},\frac {π}{3},3x^{2} - y + 3xy^{3} + x^{4} - 1,2x - y$
注意:(1)多项式的各项应包括它们前面的符号;(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的;(4)一个多项式的最高次项可以不唯一.
答案:
单项式:
$-\frac{1}{2}a^2b$:系数$-\frac{1}{2}$,次数3;
$\frac{m^4n^2}{7}$:系数$\frac{1}{7}$,次数6;
$x$:系数1,次数1;
$32t^3$:系数32,次数3;
$\frac{\pi}{3}$:系数$\frac{\pi}{3}$,次数0。
多项式:
$x^2 + y^2 - 1$:项$x^2$,$y^2$,$-1$;次数2;
$3x^2 - y + 3xy^3 + x^4 - 1$:项$3x^2$,$-y$,$3xy^3$,$x^4$,$-1$;次数4;
$2x - y$:项$2x$,$-y$;次数1。
$-\frac{1}{2}a^2b$:系数$-\frac{1}{2}$,次数3;
$\frac{m^4n^2}{7}$:系数$\frac{1}{7}$,次数6;
$x$:系数1,次数1;
$32t^3$:系数32,次数3;
$\frac{\pi}{3}$:系数$\frac{\pi}{3}$,次数0。
多项式:
$x^2 + y^2 - 1$:项$x^2$,$y^2$,$-1$;次数2;
$3x^2 - y + 3xy^3 + x^4 - 1$:项$3x^2$,$-y$,$3xy^3$,$x^4$,$-1$;次数4;
$2x - y$:项$2x$,$-y$;次数1。
【例2】判断下列说法是否正确.
(1)多项式$a^{3} - a^{2}b + ab^{2} - b^{3}$的项为$a^{3},a^{2}b,ab^{2},b^{3}$,次数为12. (
(2)多项式$3n^{4} - 2n^{2} + 1$的次数为4,常数项为1. (
(1)多项式$a^{3} - a^{2}b + ab^{2} - b^{3}$的项为$a^{3},a^{2}b,ab^{2},b^{3}$,次数为12. (
×
)(2)多项式$3n^{4} - 2n^{2} + 1$的次数为4,常数项为1. (
√
)
答案:
(1)×
(2)√
(1)×
(2)√
【例3】如果整式$x^{n - 2} - 5x + 2$是关于$x$的三次三项式,那么$n$等于(
A.3
B.4
C.5
D.6
C
).A.3
B.4
C.5
D.6
答案:
C
变式:(1)若关于$x,y$的多项式$(a - 2)x^{2} + (2b + 1)xy - x + y - 7$中不含二次项,则$ab$的值为.
(2)已知$-5x^{m} + 10^{4}x^{m} - 4x^{m}y^{2}$是关于$x,y$的六次多项式,求$m$的值,并写出该多项式.
(2)已知$-5x^{m} + 10^{4}x^{m} - 4x^{m}y^{2}$是关于$x,y$的六次多项式,求$m$的值,并写出该多项式.
答案:
(1)$-1$
(2)$m$的值为$4$,该多项式为$-5x^{4}+10^{4}x^{4}-4x^{4}y^{2}$
(1)$-1$
(2)$m$的值为$4$,该多项式为$-5x^{4}+10^{4}x^{4}-4x^{4}y^{2}$
1. 下列代数式中,哪些是整式?哪些是单项式?哪些是多项式?
$xy + z,ax^{2} + bx,-1,π,\frac {x + 1}{2},\frac {y - 1}{x}$
整式:;
单项式:;
多项式:.
$xy + z,ax^{2} + bx,-1,π,\frac {x + 1}{2},\frac {y - 1}{x}$
整式:;
单项式:;
多项式:.
答案:
整式:$xy + z$,$ax^{2} + bx$,$-1$,$\pi$,$\frac {x + 1}{2}$;
单项式:$-1$,$\pi$;
多项式:$xy + z$,$ax^{2} + bx$,$\frac {x + 1}{2}$。
单项式:$-1$,$\pi$;
多项式:$xy + z$,$ax^{2} + bx$,$\frac {x + 1}{2}$。
2. 用整式填空,指出单项式的系数、次数以及多项式的项和次数.
(1)某种苹果的售价是每千克$x$元,用面值是50元的人民币购买6千克,要花费
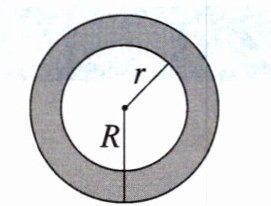
(2)用式子表示圆环的面积: .
.
(3)某种商品的原价每件为$b$元,第1次降价打8折,第2次降价每件又减10元,第1次降价后的售价是
(1)某种苹果的售价是每千克$x$元,用面值是50元的人民币购买6千克,要花费
6x
元,应找回50-6x
元.(2)用式子表示圆环的面积:


(3)某种商品的原价每件为$b$元,第1次降价打8折,第2次降价每件又减10元,第1次降价后的售价是
0.8b
元,第2次降价后的售价是0.8b-10
元.
答案:
(2)πR²-πr²
(3)0.8b (0.8b-10)
(2)πR²-πr²
(3)0.8b (0.8b-10)
查看更多完整答案,请扫码查看


