第82页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
14. 如图,在$\bigtriangleup ABC$中,$DE// FG// BC$,$GI// EH// AB$,若$\bigtriangleup ADE$,$\bigtriangleup EFG$,$\bigtriangleup GIC$的面积分别为$20$,$45$,$80$,求$\bigtriangleup ABC$的面积.
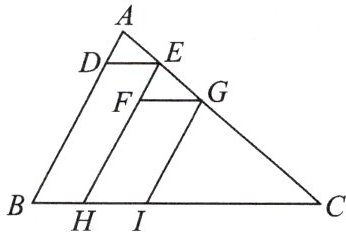

答案:
14.405.
15. (1)【问题背景】如图①,在$\bigtriangleup ABC$中,$DE// BC$分别交$AB$,$AC$于点$D$,$E$,过点$E$作$EF// AB$交$BC$于点$F$.请按图示数据填空:
四边形$DBFE$的面积$S =$
$\bigtriangleup EFC$的面积$S_1 =$
$\bigtriangleup ADE$的面积$S_2 =$
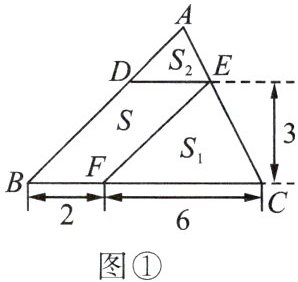
(2)【探究发现】在(1)中,若$BF = a$,$FC = b$,$DE$与$BC$间的距离为$h$,请证明$S^{2} = 4S_1S_2$.
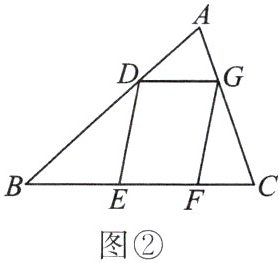
(3)【拓展迁移】如图②,$□ DEFG$的四个顶点在$\bigtriangleup ABC$的三条边上,若$\bigtriangleup ADG$,$\bigtriangleup DBE$,$\bigtriangleup GFC$的面积分别为$2$,$5$,$3$,试利用(2)中的结论求$\bigtriangleup ABC$的面积.
四边形$DBFE$的面积$S =$
6
;$\bigtriangleup EFC$的面积$S_1 =$
9
;$\bigtriangleup ADE$的面积$S_2 =$
1
.
(2)【探究发现】在(1)中,若$BF = a$,$FC = b$,$DE$与$BC$间的距离为$h$,请证明$S^{2} = 4S_1S_2$.
(3)【拓展迁移】如图②,$□ DEFG$的四个顶点在$\bigtriangleup ABC$的三条边上,若$\bigtriangleup ADG$,$\bigtriangleup DBE$,$\bigtriangleup GFC$的面积分别为$2$,$5$,$3$,试利用(2)中的结论求$\bigtriangleup ABC$的面积.

答案:
15.
(1)S=6,S1=9,S2=1.
(2)
∵DE//BC,EF//AB,
∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF.
∴△ADE∽△EFC,$\frac{S_2}{S_1}=(\frac{DE}{FC})^2=\frac{a^2}{b^2}$.
∵S1=$\frac{1}{2}$bh,
∴S2=$\frac{a^2}{b^2}· S_1=\frac{a^2h}{2b}$.
∴4S1S2=4·$\frac{1}{2}$bh·$\frac{a^2h}{2b}$=(ah)².
而S=ah,
∴S²=4S1S2.
(3)如图,过点G作GH//AB交BC于点H,则四边形DBHG为平行四边形,

∴∠GHC=∠B,BD=HG,DG=BH.
∵四边形DEFG为平行四边形,
∴DG=EF.
∴BH=EF.
∴BE=HF.
∴△DBE≌△GHF.
∴S△GHC=S△GHF+S△GFC=5+3=8.
由
(2)得,S□DBHG=2$\sqrt{2×8}$=8.
∴S△ABC=2+8+8=18.
15.
(1)S=6,S1=9,S2=1.
(2)
∵DE//BC,EF//AB,
∴四边形DBFE为平行四边形,∠AED=∠C,∠A=∠CEF.
∴△ADE∽△EFC,$\frac{S_2}{S_1}=(\frac{DE}{FC})^2=\frac{a^2}{b^2}$.
∵S1=$\frac{1}{2}$bh,
∴S2=$\frac{a^2}{b^2}· S_1=\frac{a^2h}{2b}$.
∴4S1S2=4·$\frac{1}{2}$bh·$\frac{a^2h}{2b}$=(ah)².
而S=ah,
∴S²=4S1S2.
(3)如图,过点G作GH//AB交BC于点H,则四边形DBHG为平行四边形,

∴∠GHC=∠B,BD=HG,DG=BH.
∵四边形DEFG为平行四边形,
∴DG=EF.
∴BH=EF.
∴BE=HF.
∴△DBE≌△GHF.
∴S△GHC=S△GHF+S△GFC=5+3=8.
由
(2)得,S□DBHG=2$\sqrt{2×8}$=8.
∴S△ABC=2+8+8=18.
查看更多完整答案,请扫码查看


