《2026年课堂作业武汉出版社九年级数学下册人教版》

11.某同学在为期$40$天的暑假社会实践中参与了一家网店的经营，了解到一种成本为$20$元/件的新型商品在第$x$天销售的相关信息如下表所示.

销售量$p$/件 $p = 50 - x$
销售单价$q$/(元/件) 当$1 \leq x \leq 20$时，$q = 30 + \frac{1}{2}x$；当$21 \leq x \leq 40$时，$q = 20 + \frac{525}{x}$
(1)该商品的销售单价为$35$元/件时，是第几天？
(2)求该网店第$x$天获得的利润$y$(单位：元)关于$x$的函数解析式.
(3)这$40$天中该网店第几天获得的利润最大？最大利润是多少？

答案： 11.
(1)当1≤x≤20时，
令q=30+$\frac{1}{2}$x=35,解得x=10;
　当21≤x≤40时，
　令q=20+$\frac{525}{x}$=35,解得x=35.
∴第10天或第35天该商品的销售单价为35元/件.
(2)当1≤x≤20时，y=(30+$\frac{1}{2}$x−20)(50−x)=
　−$\frac{1}{2}$x²+15x+500;
　当21≤x≤40时，y=(20+$\frac{525}{x}$−20)(50−x)=
　$\frac{26250}{x}$−525.
∴y关于x的函数解析式为
　y=$\begin{cases}-\frac{1}{2}x^{2}+15x+500(1\leqslant x\leqslant20),\frac{26250}{x}-525(21\leqslant x\leqslant40).\end{cases}$
(3)当1≤x≤20时，
　y=−$\frac{1}{2}$x²+15x+500=−$\frac{1}{2}$(x−15)²+612.5,
∵−$\frac{1}{2}$＜0,
∴当x=15时,y有最大值y1,且y1=612.5(元).
　当21≤x≤40时，
∵26250＞0,
∴$\frac{26250}{x}$的值随着x的增大而减小.
∴当x=21时,y=$\frac{26250}{21}$−525有最大值y2，且y2=$\frac{26250}{21}$−525=725(元).
∵y1＜y2,
∴这40天中该网店第21天获得的利润最大,最大利润是725元.

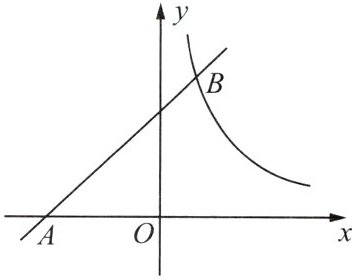
12.如图，一次函数$y = x + m$的图象经过点$A( - 3,0)$，交反比例函数$y = \frac{k}{x}$的图象于点$B(n,4)$.
(1)求$m,n,k$的值.
(2)点$C$在反比例函数$y = \frac{k}{x}$第一象限的图象上，若$S_{\bigtriangleup AOC} ＜ S_{\bigtriangleup AOB}$，直接写出点$C$的横坐标$a$的取值范围.

答案： 12.
(1)
∵一次函数y=x+m的图象经过点A(−3,0)，点B(n,4)，
∴$\begin{cases}-3+m=0,\\n+m=4.\end{cases}$
　解得$\begin{cases}m=3,\\n=1.\end{cases}$
∴点B(1,4).
∵反比例函数y=$\frac{k}{x}$的图象经过点B(1,4)，
∴k=1×4=4.
(2)
∵点A(−3,0),点B(1,4),
∴AO=3.
∴S△AOB=$\frac{1}{2}$AO×|yB|=$\frac{1}{2}$×3×4=6,S△AOC=$\frac{1}{2}$AO×|yC|=$\frac{3}{2}$yC,
　由题意得$\frac{3}{2}$yC＜6.
∴yC＜4.
∴xC＞1.
∴点C的横坐标a的取值范围为a＞1.

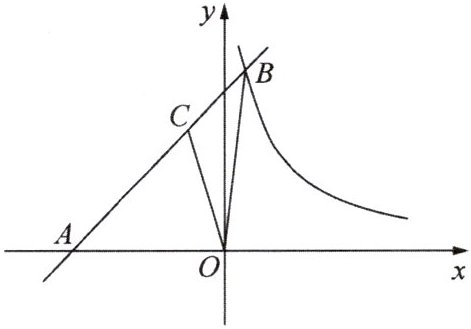
13.如图，在平面直角坐标系中，函数$y = x + b$的图象与函数$y = \frac{k}{x}(x ＞ 0)$的图象相交于点$B(1,6)$，并与$x$轴交于点$A$.点$C$是线段$AB$上一点，$\bigtriangleup OAC$与$\bigtriangleup OAB$的面积比为$2:3$.
(1)求$k$和$b$的值.
(2)若将$\bigtriangleup OAC$绕点$O$顺时针旋转，使点$C$的对应点$C^{\prime}$落在$x$轴的正半轴上，得到$\bigtriangleup OA^{\prime}C^{\prime}$，判断点$A^{\prime}$是否在函数$y = \frac{k}{x}(x ＞ 0)$的图象上，并说明理由.

答案：
13.
(1)
∵函数y=x+b的图象与函数y=$\frac{k}{x}$(x＞0)
　的图象相交于点B(1,6)，
∴6=1+b，6=$\frac{k}{1}$.
∴b=5，k=6.
(2)点A'不在函数y=$\frac{k}{x}$(x＞0)的图象上，理由如下.
　如图，过点C作CM⊥x轴于点M,过点B作BN⊥x轴于点N,过点A'作A'G⊥x轴于点G，
∵点B(1,6),
∴ON=1,BN=6.
∵△OAC与△OAB的面积比为2:3，
　$\frac{S_{\triangle OAC}}{S_{\triangle OAB}}=\frac{\frac{1}{2}OA· CM}{\frac{1}{2}OA· BN}=\frac{2}{3}$.
∴$\frac{CM}{BN}=\frac{2}{3}$.
∴CM=$\frac{2}{3}$BN=4,即点C的纵坐标为4.
　把y=4代入y=x+5，得x=−1,
∴C(−1,4).
∴OC'=OC=$\sqrt{OM^{2}+CM^{2}}=\sqrt{1^{2}+4^{2}}=\sqrt{17}$.
∵y=x+5中，当y=0时，x=−5,
∴OA=5.
　由旋转的性质，得△OAC≌△OA'C',
∴$\frac{1}{2}$OA·CM=$\frac{1}{2}$OC'·A'G.
∴A'G=$\frac{OA· CM}{OC'}=\frac{5×4}{\sqrt{17}}=\frac{20\sqrt{17}}{17}$.
　在Rt△A'OG中，
　OG=$\sqrt{A'O^{2}-A'G^{2}}=\sqrt{5^{2}-(\frac{20\sqrt{17}}{17})^{2}}=\frac{5\sqrt{17}}{17}$，
∴点A'的坐标为($\frac{5\sqrt{17}}{17}$,$\frac{20\sqrt{17}}{17}$).
∵$\frac{5\sqrt{17}}{17}$×$\frac{20\sqrt{17}}{17}$≠6,
∴点A'不在函数y=$\frac{k}{x}$(x＞0)的图象上.