第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
5. 某市举行中学生科普知识竞赛.如图,用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率$y$(该校竞赛成绩优秀的人数与该校参加竞赛人数的比值)与该校参加竞赛人数$x$的情况,其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上,则这四所学校在这次科普知识竞赛中成绩优秀人数最多的是(
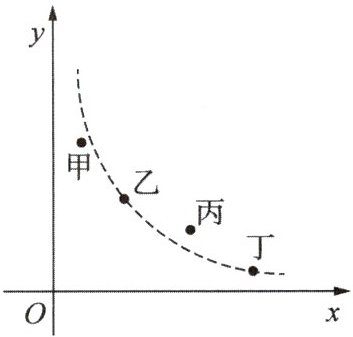
A.甲
B.乙
C.丙
D.丁
C
).
A.甲
B.乙
C.丙
D.丁
答案:
5.C
B 级
6. 充有一定质量气体的气球,根据物理学知识可知,当温度不变时,气球内的气体压强$p$(单位:$ kPa$)与气体的体积$V$(单位:$ m^3$)之间满足反比例函数关系,其图象如图所示.当气球内的气体压强大于$140\ kPa$时,气球将爆炸.为了安全起见,气球的体积应(
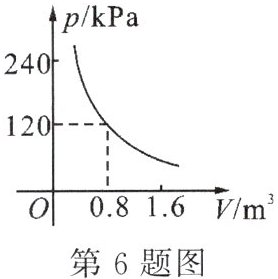
A.不大于$\frac{24}{35}\ m^3$
B.不小于$\frac{24}{35}\ m^3$
C.不大于$\frac{24}{37}\ m^3$
D.不小于$\frac{24}{37}\ m^3$
6. 充有一定质量气体的气球,根据物理学知识可知,当温度不变时,气球内的气体压强$p$(单位:$ kPa$)与气体的体积$V$(单位:$ m^3$)之间满足反比例函数关系,其图象如图所示.当气球内的气体压强大于$140\ kPa$时,气球将爆炸.为了安全起见,气球的体积应(
B
).
A.不大于$\frac{24}{35}\ m^3$
B.不小于$\frac{24}{35}\ m^3$
C.不大于$\frac{24}{37}\ m^3$
D.不小于$\frac{24}{37}\ m^3$
答案:
6.B
7. 如图,一杠杆装置的一端吊起一桶水,水桶对杆的拉力的作用点到支点的距离固定不变.甲、乙、丙、丁四位同学分别在杆的另一端施加竖直向下的压力$F_ 甲$,$F_ 乙$,$F_ 丙$,$F_ 丁$,将相同质量的水桶吊起同样的高度,若$F_ 乙 < F_ 丙 < F_ 甲 < F_ 丁$,则这四位同学对杆的压力的作用点到支点的距离最远的是(
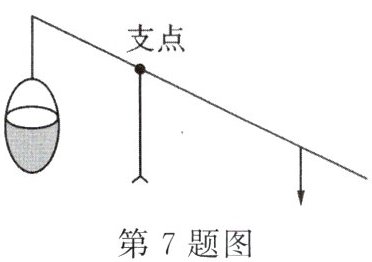
A.甲同学
B.乙同学
C.丙同学
D.丁同学
B
).
A.甲同学
B.乙同学
C.丙同学
D.丁同学
答案:
7.B
8. 如图,桌面上放置一个圆台,已知圆台的上底面积是下底面积的$\frac{1}{4}$,此时圆台对桌面的压强为$100\ Pa$.若把圆台翻过来放,则它对桌面的压强是
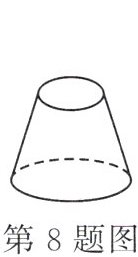
400 Pa
.
答案:
8.400 Pa
9. 如图①,电子体重秤读数直观又便于携带,为人们带来了方便.某综合实践活动小组设计了简易电子体重秤.他们制作了一个装有踏板(踏板质量忽略不计)的可变电阻$R_1$,$R_1$与踏板上人的质量$m$之间的函数关系式为$R_1 = km + b$(其中$k$,$b$为常数,$0 \leq m \leq 118$),其图象如图②所示.图③的电路图中,电源电压恒为$8\ V$,定值电阻$R_0$的阻值为$30\ \Omega$,接通开关,人站上踏板,电压表显示的读数为$U_0$,该读数可以换算出人的质量$m$.
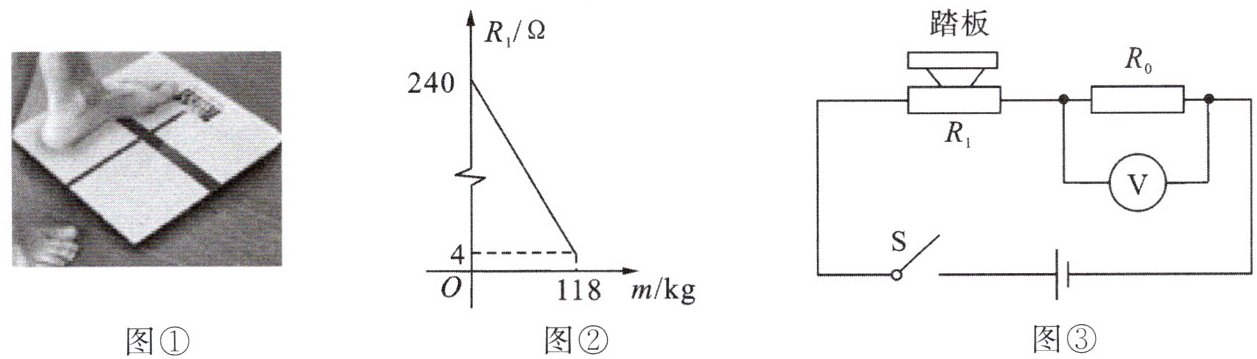
(1) 求$k$,$b$的值.
(2) 求$R_1$关于$U_0$的函数解析式.
(3) 用含$U_0$的代数式表示$m$.
(4) 若电压表的量程为$0$~$6\ V$,为保护电压表,请确定该电子体重秤可称量的最大质量.

(1) 求$k$,$b$的值.
(2) 求$R_1$关于$U_0$的函数解析式.
(3) 用含$U_0$的代数式表示$m$.
(4) 若电压表的量程为$0$~$6\ V$,为保护电压表,请确定该电子体重秤可称量的最大质量.
答案:
(1)将(0,240),(118,4)代入$R_1 = km + b$,
得$\begin{cases}b = 240,\\118k + b = 4.\end{cases}$解得$\begin{cases}k = - 2,\\b = 240.\end{cases}$
$\therefore R_1 = - 2m + 240(0\leqslant m\leqslant118)$.
(2)由题意得,可变电阻两端的电压=电源电压-电表电压,即可变电阻电压=$8 - U_0$,
$\because I = \frac{U}{R}$,可变电阻和定值电阻的电流大小相等,
$\therefore\frac{8 - U_0}{R_1} = \frac{U_0}{R_0}$,化简得$R_1 = R_0(\frac{8}{U_0} - 1)$.
$\because R_0 = 30$,$\therefore R_1 = \frac{240}{U_0} - 30$.
(3)将$R_1 = - 2m + 240(0\leqslant m\leqslant118)$代入$R_1 = \frac{240}{U_0} - 30$,得$- 2m + 240 = \frac{240}{U_0} - 30$,
化简得$m = - \frac{120}{U_0} + 135(0\leqslant m\leqslant118)$.
(4)$\because m = - \frac{120}{U_0} + 135$中$k = - 120 < 0$,且$0\leqslant U_0\leqslant6$,
$\therefore m$随$U_0$的增大而增大.
$\therefore U_0$取最大值6时,$m_{max} = - \frac{120}{6} + 135 = 115( kg)$.
$\because m = 115 < 118$,符合题意,
$\therefore m_{max} = 115 kg$.
(1)将(0,240),(118,4)代入$R_1 = km + b$,
得$\begin{cases}b = 240,\\118k + b = 4.\end{cases}$解得$\begin{cases}k = - 2,\\b = 240.\end{cases}$
$\therefore R_1 = - 2m + 240(0\leqslant m\leqslant118)$.
(2)由题意得,可变电阻两端的电压=电源电压-电表电压,即可变电阻电压=$8 - U_0$,
$\because I = \frac{U}{R}$,可变电阻和定值电阻的电流大小相等,
$\therefore\frac{8 - U_0}{R_1} = \frac{U_0}{R_0}$,化简得$R_1 = R_0(\frac{8}{U_0} - 1)$.
$\because R_0 = 30$,$\therefore R_1 = \frac{240}{U_0} - 30$.
(3)将$R_1 = - 2m + 240(0\leqslant m\leqslant118)$代入$R_1 = \frac{240}{U_0} - 30$,得$- 2m + 240 = \frac{240}{U_0} - 30$,
化简得$m = - \frac{120}{U_0} + 135(0\leqslant m\leqslant118)$.
(4)$\because m = - \frac{120}{U_0} + 135$中$k = - 120 < 0$,且$0\leqslant U_0\leqslant6$,
$\therefore m$随$U_0$的增大而增大.
$\therefore U_0$取最大值6时,$m_{max} = - \frac{120}{6} + 135 = 115( kg)$.
$\because m = 115 < 118$,符合题意,
$\therefore m_{max} = 115 kg$.
查看更多完整答案,请扫码查看


