第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
8. 【数学应用】某商场从厂家购进了$A$,$B$两种品牌篮球,第一批购买了这两种品牌篮球各$40$个,共花费了$7200$元。全部销售完后,商家打算再购进一批这两种品牌的篮球,最终第二批购进$50个A品牌篮球和30个B品牌篮球共花费了7400$元。两次购进$A$,$B$两种篮球进价保持不变。
(1)求每个$A$,$B$两种品牌篮球进价各为多少元。
(2)第二批篮球在销售过程中,$A品牌篮球每个原售价为140$元,售出$40$个后出现滞销,商场决定打折出售剩余的$A$品牌篮球;$B品牌篮球每个按进价加价30\%$销售,很快全部售出。已知第二批两种品牌篮球全部售出后共获利$2440$元,求$A$品牌篮球打几折出售。
(1)求每个$A$,$B$两种品牌篮球进价各为多少元。
(2)第二批篮球在销售过程中,$A品牌篮球每个原售价为140$元,售出$40$个后出现滞销,商场决定打折出售剩余的$A$品牌篮球;$B品牌篮球每个按进价加价30\%$销售,很快全部售出。已知第二批两种品牌篮球全部售出后共获利$2440$元,求$A$品牌篮球打几折出售。
答案:
(1)设A品牌篮球进价为x元/个,B品牌篮球进价为y元/个。
根据题意,得{40×(x+y)=7200,50x+30y=7400,解得{x=100,y=80。
所以A品牌篮球进价为100元/个,B品牌篮球进价为80元/个。
(2)设A品牌篮球打m折出售,则A品牌篮球的利润为(140-100)×40+(50-40)×140×m10-100×(50-40)=140m+600(元),
B品牌篮球的利润为30×80×30%=720(元)。
根据题意,得140m+600+720=2440,解得m=8。
所以A品牌篮球打八折出售。
(1)设A品牌篮球进价为x元/个,B品牌篮球进价为y元/个。
根据题意,得{40×(x+y)=7200,50x+30y=7400,解得{x=100,y=80。
所以A品牌篮球进价为100元/个,B品牌篮球进价为80元/个。
(2)设A品牌篮球打m折出售,则A品牌篮球的利润为(140-100)×40+(50-40)×140×m10-100×(50-40)=140m+600(元),
B品牌篮球的利润为30×80×30%=720(元)。
根据题意,得140m+600+720=2440,解得m=8。
所以A品牌篮球打八折出售。
9. 为庆祝中华人民共和国成立$76$周年,某单位请广告公司为其制作“我的祖国”文艺活动的展板、宣传册和横幅,其中制作宣传册的数量是展板数量的$5$倍,广告公司制作每件产品所需时间和利润如下表:
|产品|展板|宣传册|横幅|
|制作一件产品所需时间/h|$1$|$\frac{1}{5}$|$\frac{1}{2}$|
|制作一件产品所获利润/元|$20$|$3$|$10$|
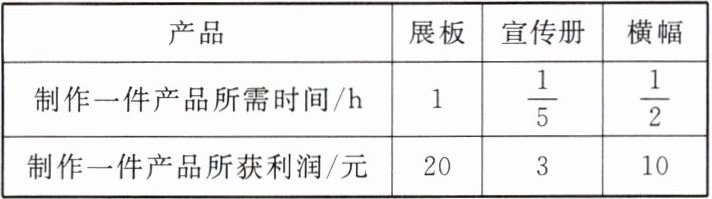
(1)若制作三种产品共计需要$25h$,所获利润为$450$元,求制作展板、宣传册和横幅的数量。
(2)若广告公司所获利润为$700$元,且三种产品均有制作。求制作三种产品总数量的最小值。
|产品|展板|宣传册|横幅|
|制作一件产品所需时间/h|$1$|$\frac{1}{5}$|$\frac{1}{2}$|
|制作一件产品所获利润/元|$20$|$3$|$10$|

(1)若制作三种产品共计需要$25h$,所获利润为$450$元,求制作展板、宣传册和横幅的数量。
(2)若广告公司所获利润为$700$元,且三种产品均有制作。求制作三种产品总数量的最小值。
答案:
(1)设制作展板数量为x,则宣传册数量为5x,横幅数量为y。
根据题意,得{20x+3×5x+10y=450,x+15×5x+12y=25,
解得{x=10,y=10,此时,5x=5×10=50。
所以制作展板、宣传册和横幅的数量分别是10,50,10。
(2)设制作展板数量为x,则宣传册数量为5x,横幅数量为y,制作三种产品总数量为w。
根据题意,得20x+3×5x+10y=700,即7x+2y=140。
所以y=140-7x2。
所以w=x+5x+y=6x+140-7x2=140+5x2=70+52x。
因为x,y取正整数,所以x可取的最小正整数为2。
所以w=70+52x的最小值为75。
所以制作三种产品总数量的最小值为75。
(1)设制作展板数量为x,则宣传册数量为5x,横幅数量为y。
根据题意,得{20x+3×5x+10y=450,x+15×5x+12y=25,
解得{x=10,y=10,此时,5x=5×10=50。
所以制作展板、宣传册和横幅的数量分别是10,50,10。
(2)设制作展板数量为x,则宣传册数量为5x,横幅数量为y,制作三种产品总数量为w。
根据题意,得20x+3×5x+10y=700,即7x+2y=140。
所以y=140-7x2。
所以w=x+5x+y=6x+140-7x2=140+5x2=70+52x。
因为x,y取正整数,所以x可取的最小正整数为2。
所以w=70+52x的最小值为75。
所以制作三种产品总数量的最小值为75。
查看更多完整答案,请扫码查看


