第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
6. 有下列计算:
① $\sqrt{(-4) × (-9)} = \sqrt{-4} × \sqrt{-9} = 6$;
② $\sqrt{(-4) × (-9)} = \sqrt{4} × \sqrt{9} = 6$;
③ $\sqrt{5^{2} - 4^{2}} = \sqrt{5 + 4} × \sqrt{5 - 4} = 3$;
④ $\sqrt{5^{2} - 4^{2}} = \sqrt{5^{2}} - \sqrt{4^{2}} = 1$。
其中正确的有(
A.1 个
B.2 个
C.3 个
D.4 个
① $\sqrt{(-4) × (-9)} = \sqrt{-4} × \sqrt{-9} = 6$;
② $\sqrt{(-4) × (-9)} = \sqrt{4} × \sqrt{9} = 6$;
③ $\sqrt{5^{2} - 4^{2}} = \sqrt{5 + 4} × \sqrt{5 - 4} = 3$;
④ $\sqrt{5^{2} - 4^{2}} = \sqrt{5^{2}} - \sqrt{4^{2}} = 1$。
其中正确的有(
B
)。A.1 个
B.2 个
C.3 个
D.4 个
答案:
B
7. 化简$(\sqrt{3} + 2)^{99} × (\sqrt{3} - 2)^{100}$的结果是(
A.-1
B.$\sqrt{3} - 2$
C.$2 - \sqrt{3}$
D.$-2 - \sqrt{3}$
C
)。A.-1
B.$\sqrt{3} - 2$
C.$2 - \sqrt{3}$
D.$-2 - \sqrt{3}$
答案:
C
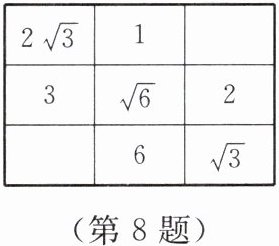
8. 【数学游戏】如图,在下面的表格中,横向、纵向及对角线方向上的实数相乘都能得到同样的结果,则两个空格中的实数之积为(
| $2\sqrt{3}$ | 1 | |
| 3 | $\sqrt{6}$ | 2 |
| | 6 | $\sqrt{3}$ |
A.$2\sqrt{2}$
B.$3\sqrt{2}$
C.$4\sqrt{2}$
D.6
D
)。| $2\sqrt{3}$ | 1 | |
| 3 | $\sqrt{6}$ | 2 |
| | 6 | $\sqrt{3}$ |

A.$2\sqrt{2}$
B.$3\sqrt{2}$
C.$4\sqrt{2}$
D.6
答案:
D
9. 计算:
(1) $\sqrt{\frac{2}{5}} × \sqrt{10} + \frac{\sqrt{32}}{\sqrt{8}}$;
(2) $(\sqrt{5} + 1)^{2} + (\sqrt{5} + 1)(\sqrt{5} - 1)$。
(1) $\sqrt{\frac{2}{5}} × \sqrt{10} + \frac{\sqrt{32}}{\sqrt{8}}$;
(2) $(\sqrt{5} + 1)^{2} + (\sqrt{5} + 1)(\sqrt{5} - 1)$。
答案:
(1)$\sqrt{\frac{2}{5}}×\sqrt{10}+\frac{\sqrt{32}}{\sqrt{8}}=\sqrt{\frac{2}{5}×10}+\sqrt{\frac{32}{8}}=2+2=4$;
(2)$(\sqrt{5}+1)^{2}+(\sqrt{5}+1)(\sqrt{5}-1)=5+2\sqrt{5}+1+5-1=10+2\sqrt{5}$。
(1)$\sqrt{\frac{2}{5}}×\sqrt{10}+\frac{\sqrt{32}}{\sqrt{8}}=\sqrt{\frac{2}{5}×10}+\sqrt{\frac{32}{8}}=2+2=4$;
(2)$(\sqrt{5}+1)^{2}+(\sqrt{5}+1)(\sqrt{5}-1)=5+2\sqrt{5}+1+5-1=10+2\sqrt{5}$。
10. 【跨学科】在平整的路面上,某型号汽车紧急刹车后仍会滑行 $s$ m,一般地,有经验公式 $s = \frac{v^{2}}{300}$,其中 $v$ 表示刹车前汽车的速度(单位:km/h)。一次行驶中汽车紧急刹车后滑行的距离 $s = 12$ m,则这辆汽车刹车前的速度 $v = $
60
km/h。
答案:
60
11. 【数学文化】我国古代数学家秦九韶曾记述了“三斜求积术”,即已知三角形的三边长,求它的面积。用符号表示即为:$S = \sqrt{\frac{1}{4}[a^{2}b^{2} - (\frac{a^{2} + b^{2} - c^{2}}{2})^{2}]}$(其中 $a$,$b$,$c$ 为三角形的三边长,$S$ 为面积)。请利用这个公式求当 $a = \sqrt{5}$,$b = 3$,$c = 2\sqrt{5}$ 时的三角形的面积。
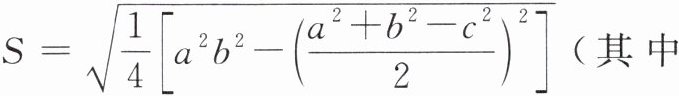
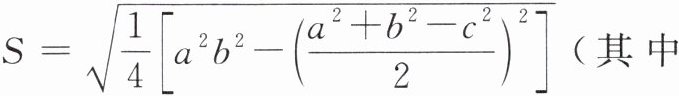
答案:
当$a=\sqrt{5}$,$b=3$,$c=2\sqrt{5}$时,$a^{2}=5$,$b^{2}=9$,$c^{2}=20$,所以$S=\sqrt{\frac{1}{4}×\left[5×9-\left(\frac{5+9-20}{2}\right)^{2}\right]}=\sqrt{\frac{1}{4}×\left[45-(-3)^{2}\right]}=\sqrt{\frac{1}{4}×(45-9)}=\sqrt{\frac{1}{4}×36}=3$。所以三角形的面积为3。
查看更多完整答案,请扫码查看


