第101页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
9. 在长方形 $ ABCD $ 中,放入六个形状、大小相同的长方形,所标尺寸如图所示。设小长方形的长、宽分别为 $ x $ cm,$ y $ cm,根据题意列出的方程组是(
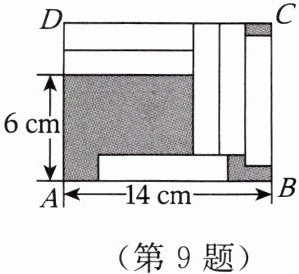
A.$\begin{cases}x - 2y + y = 6, \\ x + 3y = 14\end{cases} $
B.$\begin{cases}x + 3y = 14, \\ x + 2y = 6\end{cases} $
C.$\begin{cases}x + 3y = 14, \\ 2x - y = 6\end{cases} $
D.$\begin{cases}x + 3y = 14, \\ x + y = 6\end{cases} $
A
)。
A.$\begin{cases}x - 2y + y = 6, \\ x + 3y = 14\end{cases} $
B.$\begin{cases}x + 3y = 14, \\ x + 2y = 6\end{cases} $
C.$\begin{cases}x + 3y = 14, \\ 2x - y = 6\end{cases} $
D.$\begin{cases}x + 3y = 14, \\ x + y = 6\end{cases} $
答案:
A
10. 小华从家到学校的路是一段平路和一段下坡路。假设他始终保持平路每分钟走 60 m,下坡路每分钟走 80 m,上坡路每分钟走 40 m,则他从家到学校需 10 min,从学校到家需 15 min。请解答下列问题:
(1)小华家离学校有多远?
(2)小华从家到学校到达全程一半位置处的时间与小华从学校到家到达全程一半位置处的时间会一样吗?如果不一样,哪种情况所花的时间更多?请通过计算说明理由。
(1)小华家离学校有多远?
(2)小华从家到学校到达全程一半位置处的时间与小华从学校到家到达全程一半位置处的时间会一样吗?如果不一样,哪种情况所花的时间更多?请通过计算说明理由。
答案:
(1)设小华从家到学校的这段平路长为x m,下坡路长为y m。根据题意,得{x/60+y/80=10,x/60+y/40=15},解得{x=300,y=400}。所以x+y=700。所以小华家离学校700 m。
(2)不一样。第二种情况所花的时间更多。理由如下:全程一半位置处距离小华家和学校的距离为700÷2=350(m)。小华从家到学校到达全程一半位置处所需的时间为300÷60+(350 - 300)÷80=5.625(min);小华从学校到家到达全程一半位置处所需的时间为350÷40=8.75(min)。因为8.75 > 5.625,所以,小华从学校到家到达全程一半位置处的时间比小华从家到学校到达全程一半位置处的时间要多一些。
(1)设小华从家到学校的这段平路长为x m,下坡路长为y m。根据题意,得{x/60+y/80=10,x/60+y/40=15},解得{x=300,y=400}。所以x+y=700。所以小华家离学校700 m。
(2)不一样。第二种情况所花的时间更多。理由如下:全程一半位置处距离小华家和学校的距离为700÷2=350(m)。小华从家到学校到达全程一半位置处所需的时间为300÷60+(350 - 300)÷80=5.625(min);小华从学校到家到达全程一半位置处所需的时间为350÷40=8.75(min)。因为8.75 > 5.625,所以,小华从学校到家到达全程一半位置处的时间比小华从家到学校到达全程一半位置处的时间要多一些。
11. 【综合与实践】小明准备了一个长方体的无盖容器和 $ A $,$ B $ 两种型号的钢球若干。先往容器里加入一定量的水,如图,水高度为 30 mm,水足以淹没所有的钢球。
(1)探究一:小明做了两次实验,先放入 3 个 $ A $ 型号钢球,水面的高度涨到 36 mm;把 3 个 $ A $ 型号钢球捞出,再放入 2 个 $ B $ 型号钢球,水面的高度恰好也涨到 36 mm。据此可知:放入一个 $ A $ 型号钢球水面会上升
(2)探究二:小明把之前的钢球全部捞出,然后再放入 $ A $ 型号与 $ B $ 型号钢球共 10 个后,水面高度涨到 57 mm,求放入水中的 $ A $ 型号与 $ B $ 型号钢球各几个。
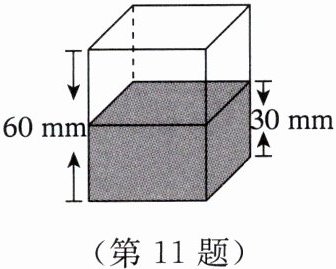
(1)探究一:小明做了两次实验,先放入 3 个 $ A $ 型号钢球,水面的高度涨到 36 mm;把 3 个 $ A $ 型号钢球捞出,再放入 2 个 $ B $ 型号钢球,水面的高度恰好也涨到 36 mm。据此可知:放入一个 $ A $ 型号钢球水面会上升
2
mm,放入一个 $ B $ 型号钢球水面会上升3
mm。(2)探究二:小明把之前的钢球全部捞出,然后再放入 $ A $ 型号与 $ B $ 型号钢球共 10 个后,水面高度涨到 57 mm,求放入水中的 $ A $ 型号与 $ B $ 型号钢球各几个。
解:设放入水中的A型号与B型号钢球分别为x个,y个。根据题意,得{x+y=10,2x+3y=57 - 30},解得{x=3,y=7}。所以放入水中的A型号钢球3个,B型号钢球7个。

答案:
(1)2 3 解析:放入一个A型号钢球水面会上升(36 - 30)÷3=2(mm);放入一个B型号钢球水面会上升(36 - 30)÷2=3(mm)。
(2)解:设放入水中的A型号与B型号钢球分别为x个,y个。根据题意,得{x+y=10,2x+3y=57 - 30},解得{x=3,y=7}。所以放入水中的A型号钢球3个,B型号钢球7个。
(1)2 3 解析:放入一个A型号钢球水面会上升(36 - 30)÷3=2(mm);放入一个B型号钢球水面会上升(36 - 30)÷2=3(mm)。
(2)解:设放入水中的A型号与B型号钢球分别为x个,y个。根据题意,得{x+y=10,2x+3y=57 - 30},解得{x=3,y=7}。所以放入水中的A型号钢球3个,B型号钢球7个。
查看更多完整答案,请扫码查看


