第119页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 某快递公司快递员本周投放快递物品件数为:有3天是20件,有1天是31件,有3天是35件。本周的日平均投递物品件数为(
A.31
B.30
C.29
D.28
D
)。A.31
B.30
C.29
D.28
答案:
D
2. 小冬骑自行车的速度是15km/h,步行的速度是5km/h。
(1)如果小冬先骑自行车1h,然后又步行了1h,求他的平均速度;
(2)如果小冬先骑自行车2h,然后又步行了3h,求他的平均速度;
(3)举例说明加权平均数在生活中的应用。
(1)如果小冬先骑自行车1h,然后又步行了1h,求他的平均速度;
(2)如果小冬先骑自行车2h,然后又步行了3h,求他的平均速度;
(3)举例说明加权平均数在生活中的应用。
答案:
解:
(1)(15+5)÷2=10(km/h)。所以他的平均速度是10 km/h。
(2)(15×2+5×3)÷(2+3)=45÷5=9(km/h)。所以他的平均速度是9 km/h。
(3)略
(1)(15+5)÷2=10(km/h)。所以他的平均速度是10 km/h。
(2)(15×2+5×3)÷(2+3)=45÷5=9(km/h)。所以他的平均速度是9 km/h。
(3)略
1. 某超市销售A,B,C,D四种矿泉水,它们的单价依次是5元、4元、3元、2元。某天的销售情况如图,则这天销售的矿泉水的平均单价为(
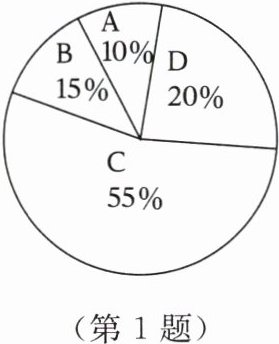
A.2.8元
B.2.85元
C.3.15元
D.3.55元
]
C
)。
A.2.8元
B.2.85元
C.3.15元
D.3.55元
]
答案:
C
2. 为了解学生参与家务劳动的情况,某班随机调查了10名学生一周做家务劳动的时间,数据如下表:

则这10名学生一周做家务劳动的平均时间是(
A.3.5h
B.3h
C.2.5h
D.2h

则这10名学生一周做家务劳动的平均时间是(
D
)。A.3.5h
B.3h
C.2.5h
D.2h
答案:
D
3. 八年级(1)班有学生50人,八年级(2)班有学生45人。在期中数学学业质量诊断中,八年级(1)班学生的平均成绩是87.5分,八年级(2)班学生的平均成绩是83.4分,则这两个班95名同学的平均成绩约为
85.6
分。(结果精确到0.1分)
答案:
85.6
4. 某广告公司欲招聘广告策划人员一名,对A,B,C三名候选人进行了三项综合素质测试。他们的各项测试成绩如下表所示:
|测试项目|测试成绩/分|
| |A|B|C|
|创新|72|50|88|
|综合知识|85|74|45|
|语言|67|70|67|
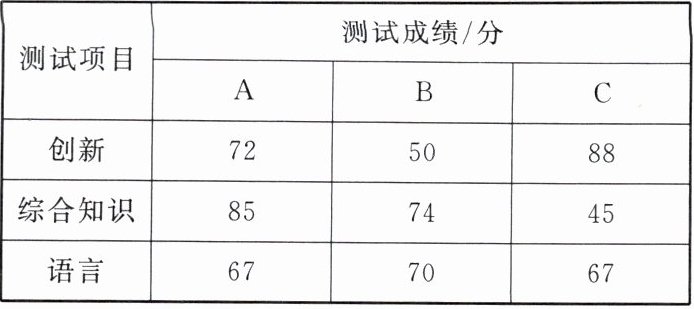
(1)如果根据三项测试的平均成绩确定人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4:3:1的比例确定每人的测试成绩,此时谁将被录用?
|测试项目|测试成绩/分|
| |A|B|C|
|创新|72|50|88|
|综合知识|85|74|45|
|语言|67|70|67|

(1)如果根据三项测试的平均成绩确定人选,那么谁将被录用?
(2)根据实际需要,公司将创新、综合知识和语言三项测试得分按4:3:1的比例确定每人的测试成绩,此时谁将被录用?
答案:
(1)$\overline{x}_{A}=\frac{72+85+67}{3}=\frac{224}{3}$,$\overline{x}_{B}=\frac{50+74+70}{3}=\frac{194}{3}$,$\overline{x}_{C}=\frac{88+45+67}{3}=\frac{200}{3}$,因为$\frac{194}{3}<\frac{200}{3}<\frac{224}{3}$,所以候选人A将被录用。
(2)A的成绩为$\frac{72×4+85×3+67×1}{4+3+1}=\frac{610}{8}$;B的成绩为$\frac{50×4+74×3+70×1}{4+3+1}=\frac{492}{8}$;C的成绩为$\frac{88×4+45×3+67×1}{4+3+1}=\frac{554}{8}$。因为$\frac{492}{8}<\frac{554}{8}<\frac{610}{8}$,所以候选人A将被录用。
(1)$\overline{x}_{A}=\frac{72+85+67}{3}=\frac{224}{3}$,$\overline{x}_{B}=\frac{50+74+70}{3}=\frac{194}{3}$,$\overline{x}_{C}=\frac{88+45+67}{3}=\frac{200}{3}$,因为$\frac{194}{3}<\frac{200}{3}<\frac{224}{3}$,所以候选人A将被录用。
(2)A的成绩为$\frac{72×4+85×3+67×1}{4+3+1}=\frac{610}{8}$;B的成绩为$\frac{50×4+74×3+70×1}{4+3+1}=\frac{492}{8}$;C的成绩为$\frac{88×4+45×3+67×1}{4+3+1}=\frac{554}{8}$。因为$\frac{492}{8}<\frac{554}{8}<\frac{610}{8}$,所以候选人A将被录用。
查看更多完整答案,请扫码查看


