第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 如图,制作一个长80cm、宽60cm的长方形木框,需在对角的顶点间钉一根木条用来加固,这根木条的长至少为
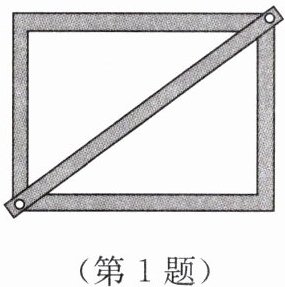
100
cm。
答案:
100
2. 如图,在△ABC中,∠ACB= 90°,分别以AC,AB为边向外作正方形,面积分别为$S_1,S_2。$若$S_1= 2,S_2= 6,$则BC=

2
。
答案:
2
3. 如图所示的是某公园一角的示意图,有人为了抄近道而避开路的拐角∠ABC(∠ABC= 90°),在草坪内走出了一条不该有的“捷径AC”。已知AB= 8m,BC= 6m,他们踩坏了长
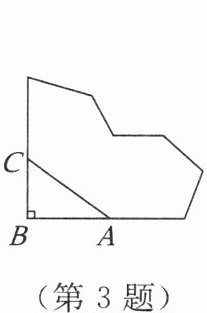
10
m的草坪,只为少走4
m的路。
答案:
10 4
4. 如图,在△ABC中,∠C= 90°,AP是△ABC的角平分线,AC= 4,PC= 2,则点P到AB的距离等于
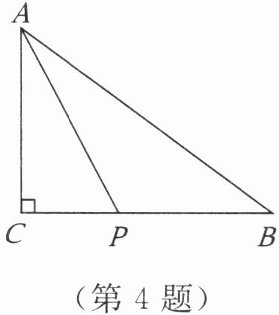
2
。
答案:
2
1. 如图所示的是由两个直角三角形和三个正方形组成的图形,图中阴影部分的面积为(
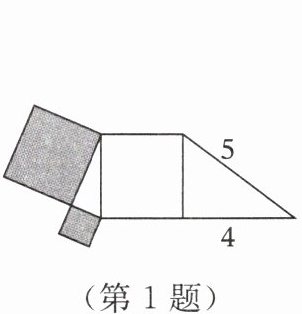
A.9
B.12
C.18
D.25
A
)。
A.9
B.12
C.18
D.25
答案:
A
2. 小明从家出发向正东方向走了600m,接着向正北方向走了800m,这时小明离家
1000
m。
答案:
1000
3. 如图,某自动感应门的正上方装着一个感应器,离地2.5m,当物体进入感应器的感应范围内时,感应门就会自动打开。一个身高1.6m的学生正对门,缓慢走到离门1.2m的地方时,感应门才自动打开,则感应器的感应距离为

1.5
m。
答案:
1.5
4. 小颖爸爸为了丰富社区小朋友的日常生活,搭了一架简易秋千,示意图如下,秋千AB在静止位置时,下端B距地面0.6m,即OB= 0.6m,当秋千荡到AC的位置时,下端C距地面1.4m,即CD= 1.4m,与静止位置的水平距离OD= 2.4m,求秋千AB的长。


答案:
解:如图,过点C作CE⊥AB于点E。
设秋千AB的长为xm,则AE=x−(1.4−0.6)=(x−0.8)m。
在Rt△AEC中,由勾股定理,得x²=(x−0.8)²+2.4²,即1.6x=6.4,解得x=4。
所以秋千AB的长为4m。

解:如图,过点C作CE⊥AB于点E。
设秋千AB的长为xm,则AE=x−(1.4−0.6)=(x−0.8)m。
在Rt△AEC中,由勾股定理,得x²=(x−0.8)²+2.4²,即1.6x=6.4,解得x=4。
所以秋千AB的长为4m。

查看更多完整答案,请扫码查看


