《2025年伴你学北京师范大学出版社八年级数学上册北师大版山西专版》

8. 【跨学科】某医药研究所开发一种新药,在试验药效时发现,如果成人按规定剂量服用,那么每毫升血液中含药量 $ y $(单位：$ \mu \mathrm{g} $)随 $ x $(单位：$ \mathrm{h} $)的变化情况如图。

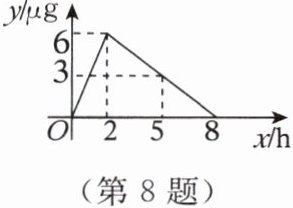
(1) 服药后 2 $ \mathrm{h} $ 血液中含药量最高,达每毫升 6 $ \mu \mathrm{g} $,接着逐步衰减；
(2) 服药后 $ 5 \mathrm{~h} $,血液中含药量为每毫升 3 $ \mu \mathrm{g} $；
(3) 当 $ x \leq 2 $ 时,$ y $ 与 $ x $ 之间的函数关系式是 y=3x；
(4) 当 $ x \geq 2 $ 时,$ y $ 与 $ x $ 之间的函数关系式是 y=-x+8；
(5) 如果每毫升血液中含药量 $ 3 \mu \mathrm{g} $ 或 $ 3 \mu \mathrm{g} $ 以上时,治疗疾病最有效,那么这个有效时间范围是 1≤x≤5。

答案：
(1)2 6
(2)3
(3)y=3x
(4)y=-x+8
(5)1≤x≤5

9. 【综合实践】有言道：“杆秤一头称起人间生计,一头称起天地良心”,某兴趣小组利用物理中的杠杆原理制作简易杆秤,同学们先设计方案,然后动手制作,再结合实际进行调试。请完成下列方案设计中的任务：
【知识背景】如图,称重物时,移动秤砣可使杆秤平衡,根据杠杆原理得 $ (m_0 + m) \cdot l = M \cdot (a + y) $,其中秤盘质量 $ m_0 \mathrm{~g} $,重物质量 $ m \mathrm{~g} $,秤砣质量 $ M \mathrm{~g} $,秤纽与秤盘的水平距离为 $ l \mathrm{~cm} $,秤纽与零刻线的水平距离为 $ a \mathrm{~cm} $,秤砣与零刻线的水平距离为 $ y \mathrm{~cm} $。
【方案设计】设计简易杆秤。设定 $ m_0 = 10 $,$ M = 50 $,最大可称重物质量为 $ 1000 \mathrm{~g} $,零刻线与末刻线的距离定为 $ 50 \mathrm{~cm} $。
任务一：确定 $ l $ 和 $ a $ 的值。
(1) 当秤盘不放重物,秤砣在零刻线时,杆秤平衡,请列出关于 $ l,a $ 的方程；
(2) 当秤盘放入质量为 $ 1000 \mathrm{~g} $ 的重物,秤砣从零刻线移至末刻线时,杆秤平衡,请列出关于 $ l,a $ 的方程；
(3) 根据(1)和(2)列出的方程,求 $ l $ 和 $ a $ 的值；
任务二：确定刻线的位置。
(4) 根据任务一,求 $ y $ 关于 $ m $ 的函数表达式；
(5) 从零刻线开始,每隔 $ 100 \mathrm{~g} $ 在秤杆上找到对应刻线,请写出相邻刻线间的距离。
]

答案：
(1)根据题意，得m=0，y=0。因为m0=10，M=50，所以10l=50a，所以l=5a。
(2)根据题意，得m=1000，y=50。所以(10+1000)l=50(a+50)，所以101l-5a=250。
(3)将l=5a代入101l-5a=250，得101l-l=250，解得l=2.5，从而a=0.5。
(4)由
(3)得l=2.5，a=0.5。所以2.5(10+m)=50(0.5+y)，所以y=1/20m。
(5)在y=1/20m中，当m=0时，y=0；当m=100时，y=5；当m=200时，y=10；当m=300时，y=15；当m=400时，y=20；当m=500时，y=25；当m=600时，y=30；当m=700时，y=35；当m=800时，y=40；当m=900时，y=45；当m=1000时，y=50。所以相邻刻线间的距离为5cm。