第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
10. 如图,在平面直角坐标系中有一张透明的三角形纸片 $ AOB $,顶点 $ A $, $ B $ 的坐标分别为 $ A(-6,0) $, $ B(0,8) $,点 $ O $ 为坐标原点。
(1) 求边 $ AB $ 的长;
(2) 设 $ C $ 是线段 $ OB $ 上一点,沿线段 $ AC $ 所在直线折叠 $ \triangle AOB $,使点 $ O $ 落在边 $ AB $ 上的点 $ D $ 处,求点 $ C $ 的坐标。
]
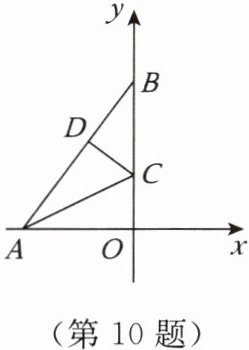
(1) 求边 $ AB $ 的长;
(2) 设 $ C $ 是线段 $ OB $ 上一点,沿线段 $ AC $ 所在直线折叠 $ \triangle AOB $,使点 $ O $ 落在边 $ AB $ 上的点 $ D $ 处,求点 $ C $ 的坐标。
]

答案:
解:
(1)因为A(-6,0),B(0,8),所以OA=6,OB=8,由勾股定理,得AB=10。
(2)设OC=x,由折叠的性质,得AD=AO=6,CD=OC=x,∠BDC=90°,所以BD=AB-AD=4,BC=8-x。在Rt△BDC中,由勾股定理,得4²+x²=(8-x)²。解得x=3。所以点C的坐标为(0,3)。
(1)因为A(-6,0),B(0,8),所以OA=6,OB=8,由勾股定理,得AB=10。
(2)设OC=x,由折叠的性质,得AD=AO=6,CD=OC=x,∠BDC=90°,所以BD=AB-AD=4,BC=8-x。在Rt△BDC中,由勾股定理,得4²+x²=(8-x)²。解得x=3。所以点C的坐标为(0,3)。
11. 【数学应用】某校计划将同学们捐赠的学习用品与图书寄往山区小学,调查发现,甲、乙两家快递公司的收费标准分别如下:
甲公司:物品不超过 $ 1 $ kg,按 $ 10 $ 元收费;超过 $ 1 $ kg,超过的部分按每千克 $ 15 $ 元收费。
乙公司:按每千克 $ 14 $ 元收费,另加包装费 $ 3 $ 元。
设需要快递的物品重 $ x $ kg,请解决下列问题:
(1) 甲、乙两家快递公司快递该物品的费用 $ y $(单位:元)与 $ x $(单位:kg)之间的函数关系式如下,请补写空缺部分:
甲公司:$ y = \begin{cases} 10(0 < x \leq 1), \\ \underline{\quad\quad\quad\quad}(x > 1); \end{cases} $
乙公司:$ y = \underline{\quad\quad\quad\quad}(x > 0) $。
(2) 假设要寄出 $ 50 $ 千克物品,试判断选哪家公司更合算。
(1)甲公司:$ y = \begin{cases} 10(0 < x \leq 1), \\ \underline{
乙公司:$ y = \underline{
(2)
甲公司:物品不超过 $ 1 $ kg,按 $ 10 $ 元收费;超过 $ 1 $ kg,超过的部分按每千克 $ 15 $ 元收费。
乙公司:按每千克 $ 14 $ 元收费,另加包装费 $ 3 $ 元。
设需要快递的物品重 $ x $ kg,请解决下列问题:
(1) 甲、乙两家快递公司快递该物品的费用 $ y $(单位:元)与 $ x $(单位:kg)之间的函数关系式如下,请补写空缺部分:
甲公司:$ y = \begin{cases} 10(0 < x \leq 1), \\ \underline{\quad\quad\quad\quad}(x > 1); \end{cases} $
乙公司:$ y = \underline{\quad\quad\quad\quad}(x > 0) $。
(2) 假设要寄出 $ 50 $ 千克物品,试判断选哪家公司更合算。
(1)甲公司:$ y = \begin{cases} 10(0 < x \leq 1), \\ \underline{
15x - 5
}(x > 1); \end{cases} $乙公司:$ y = \underline{
14x + 3
}(x > 0) $。(2)
当x=50时,甲公司:因为x>1,所以y=15x-5=15×50-5=745;乙公司:y=14x+3=14×50+3=703。因为745>703,所以选择乙快递公司更合算。
答案:
解:
(1)甲公司:当x>1时,y=10+15(x-1)=15x-5;乙公司:y=14x+3。
(2)当x=50时,甲公司:因为x>1,所以y=15x-5=15×50-5=745;乙公司:y=14x+3=14×50+3=703。因为745>703,所以选择乙快递公司更合算。
(1)甲公司:当x>1时,y=10+15(x-1)=15x-5;乙公司:y=14x+3。
(2)当x=50时,甲公司:因为x>1,所以y=15x-5=15×50-5=745;乙公司:y=14x+3=14×50+3=703。因为745>703,所以选择乙快递公司更合算。
12. 如图,一次函数 $ y = 2x + 6 $ 的图象与 $ x $ 轴交于点 $ A $,与 $ y $ 轴交于点 $ B $, $ C(m,4) $ 是直线 $ AB $ 上的一点,过点 $ C $ 作直线 $ CD // x $ 轴交 $ y $ 轴于点 $ D $。
(1) 求点 $ C $ 的坐标及 $ AB $ 的长。
(2) 已知 $ P $ 是直线 $ CD $ 上一点。
① 若 $ \triangle POC $ 的面积为 $ 4 $,求点 $ P $ 的坐标;
② 若 $ \triangle POC $ 是直角三角形,请直接写出所有满足条件的点 $ P $ 的坐标。
]

(1) 求点 $ C $ 的坐标及 $ AB $ 的长。
(2) 已知 $ P $ 是直线 $ CD $ 上一点。
① 若 $ \triangle POC $ 的面积为 $ 4 $,求点 $ P $ 的坐标;
② 若 $ \triangle POC $ 是直角三角形,请直接写出所有满足条件的点 $ P $ 的坐标。
]

答案:
解:
(1)把点C(m,4)的坐标代入y=2x+6得2m+6=4,解得m=-1,所以C(-1,4)。在Rt△AOB中,易得OA=3,OB=6,由勾股定理,得AB=√(OA²+OB²)=√(3²+6²)=3√5。
(2)①因为OD⊥CP,所以S△POC=1/2·CP·OD=4。因为OD=4,所以CP=2,所以点P的坐标为(-3,4)或(1,4)。②因为∠OCP一定不是直角,所以当∠OPC=90°时,点P恰好在点D,所以P₁(0,4)。当∠COP为直角时,因为直线OC的函数表达式为y=-4x,所以直线OP的函数表达式为y=1/4x,所以当y=4时,由1/4x=4得x=16,所以P₂(16,4)。所以满足条件的点P的坐标为(0,4)或(16,4)。
(1)把点C(m,4)的坐标代入y=2x+6得2m+6=4,解得m=-1,所以C(-1,4)。在Rt△AOB中,易得OA=3,OB=6,由勾股定理,得AB=√(OA²+OB²)=√(3²+6²)=3√5。
(2)①因为OD⊥CP,所以S△POC=1/2·CP·OD=4。因为OD=4,所以CP=2,所以点P的坐标为(-3,4)或(1,4)。②因为∠OCP一定不是直角,所以当∠OPC=90°时,点P恰好在点D,所以P₁(0,4)。当∠COP为直角时,因为直线OC的函数表达式为y=-4x,所以直线OP的函数表达式为y=1/4x,所以当y=4时,由1/4x=4得x=16,所以P₂(16,4)。所以满足条件的点P的坐标为(0,4)或(16,4)。
查看更多完整答案,请扫码查看


