《2025年伴你学北京师范大学出版社八年级数学上册北师大版山西专版》

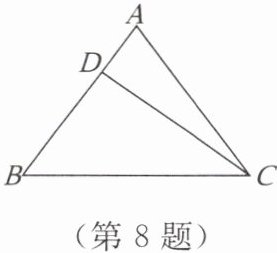
8. 已知等腰三角形 ABC 的底边 BC = 20 cm,D 是腰 AB 上一点,CD = 16 cm,BD = 12 cm。
(1)试说明：CD ⊥ AB；
(2)求△ABC 的腰长。

答案：
(1)因为BC=20cm,CD=16cm,BD=12cm,满足BD²+CD²=BC²,所以∠BDC=90°,即CD⊥AB。
(2)设△ABC的腰长为x,则AD=x - 12。由
(1)可知∠ADC=90°。由勾股定理,得AD²+CD²=AC²,即(x - 12)²+16²=x²,解得x=$\frac{50}{3}$。所以△ABC的腰长为$\frac{50}{3}$cm。

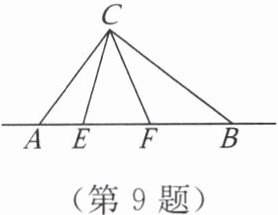
9. 【数学应用】在沿海地区,台风是一种常见的自然现象,它以台风中心为圆心在周围上千米的范围内形成极端气候,有时具有极强的破坏力。如图,一台风中心沿东西方向 AB 由 A 驶向 B,已知点 C 为一海港,点 C 与直线 AB 上 A,B 两点的距离分别为 AC = 300 km,BC = 400 km,AB = 500 km,以台风中心为圆心,周围 250 km 以内为受影响区域。
(1)求∠ACB 的度数。
(2)海港 C 受台风影响吗？为什么？
(3)若台风的速度为 20 km/h,当台风运动到点 E 处时,海港 C 刚好受到影响,当台风运动到点 F 时,海港 C 刚好不受影响,即 CE = CF = 250 km,求台风影响该海港持续的时间。

答案：
(1)因为AC=300km,BC=400km,AB=500km,所以AC²+BC²=AB²。所以△ABC是直角三角形,且∠ACB=90°。
(2)海港C受台风影响。理由如下:如图,过点C作CD⊥AB于点D。因为△ABC是直角三角形,所以由面积公式得$\frac{1}{2}$AC×BC=$\frac{1}{2}$CD×AB。所以300×400=500×CD,所以CD=240km。因为以台风中心为圆心,周围250km以内为受影响区域,所以海港C受台风影响。
(3)当CE=CF=250km时,正好影响C港口。如图,在Rt△CED中,由勾股定理,得CE²=CD²+ED²,解得ED=70km,所以EF=140km。因为台风的速度为20km/h,所以140÷20=7(h)。所以台风影响该海港持续的时间为7h。

10. 观察下表所给的三个数 a,b,c,且 a ＜ b ＜ c：

(1)试找出它们的共同点,并说明你的结论；
(2)当 a = 21 时,求 b,c 的值。

答案：
(1)题表各组数的共同点可以从以下几个方面分析:①题表各组数均满足a²+b²=c²;②最小的数a是奇数,其余的两个数是连续的正整数;③最小数a的平方等于另两个连续整数的和,如3²=9=4+5,5²=25=12+13,7²=49=24+25,9²=81=40+41,…。由以上特点我们可猜想并说明这样一个结论:设m为大于1的奇数,将m²拆分为两个连续的整数之和,即m²=n+(n+1),则m,n,n+1就构成一组简单的勾股数。因为m²=n+(n+1)(m为大于1的奇数),所以m²+n²=2n+1+n²=(n+1)²,所以m,n,n+1是一组勾股数。
(2)当a=21时,因为21²=441=220+221,所以b=220,c=221。