《2025年伴你学北京师范大学出版社八年级数学上册北师大版山西专版》

1. 【跨学科】一种弹簧秤最大能称不超过 $ 10 \mathrm{~kg} $ 的物体,不挂物体时弹簧的长为 $ 12 \mathrm{~cm} $,每挂重 $ 1 \mathrm{~kg} $ 物体,弹簧伸长 $ 0.5 \mathrm{~cm} $。在弹性限度内,挂重物后弹簧的长度 $ y $(单位：$ \mathrm{cm} $)与所挂物体的质量 $ x $(单位：$ \mathrm{kg} $)之间的函数关系式为(B)。
A.$ y = 12 - 0.5x $
B.$ y = 12 + 0.5x $
C.$ y = 10 + 0.5x $
D.$ y = 0.5x $

答案： B

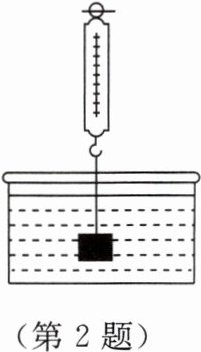
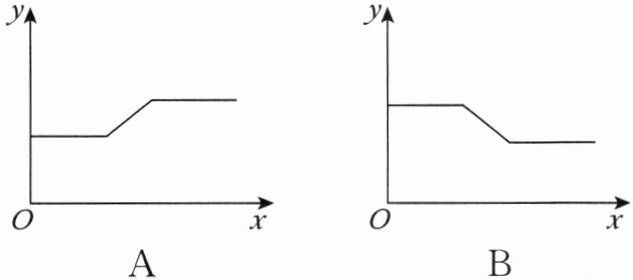
2. 【跨学科】如图,用弹簧测力计将一铁块悬挂于盛有水的水槽中,然后匀速向上提起,使铁块完全露出水面,并上升一定高度。下列能反映弹簧测力计的读数 $ y $(单位：$ \mathrm{N} $)与铁块被提起的时间 $ x $(单位：$ \mathrm{s} $)之间函数关系的图象大致是(A)。


A.
B.
C.
D.]

答案： A 解析：由浮力知识得F拉力=G-F浮力，读数y即为F拉力。在铁块露出水面以前，浮力不变，则此过程中弹簧的读数不变；当铁块慢慢露出水面开始，浮力减小，则拉力增加，弹簧的读数逐渐增大；当铁块完全露出水面后，浮力等于0，拉力等于重力，弹簧的读数不变。观察题中四个选项可知，只有选项A符合。

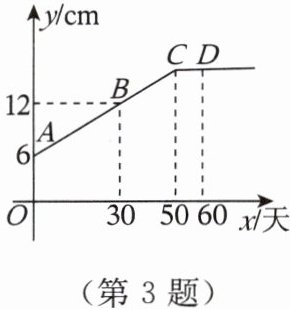
3. 【跨学科】某生物小组观察一植物生长,得到植物高度 $ y $(单位：$ \mathrm{cm} $)与观察时间 $ x $(单位：天)之间的关系,并画出如图所示的图象($ AC $ 是线段,射线 $ CD $ 平行于 $ x $ 轴)。
(1) 该植物从开始观察时起多少天以后停止长高；
(2) 求线段 $ AC $ 对应的函数表达式,并求该植物最高长到多少厘米。
]

答案：
(1)因为CD平行于x轴，所以从开始观察时起第50天以后该植物停止长高。
(2)因为点A(0,6)在直线AC上，所以设直线AC对应的函数表达式为y=kx+6。将点B(30,12)的坐标代入，得30k+6=12，解得k=1/5。所以线段AC对应的函数表达式为y=1/5x+6(0≤x≤50)。当x=50时，y=1/5×50+6=16(cm)。所以线段AC对应的函数表达式为y=1/5x+6(0≤x≤50)，该植物最高长到16cm。

1. 【数学应用】如图所示的是小明去公园锻炼及沿原路返回时离家的路程 $ y $(单位：$ \mathrm{km} $)与时间 $ t $(单位：$ \mathrm{min} $)之间的函数图象。下列结论正确的是(D)。

A.去时用的时间小于回家时用的时间
B.在公园锻炼了 $ 40 \mathrm{~min} $
C.去时走上坡路,回家时走下坡路
D.去时的速度比回家时的速度慢
]

答案： D