第56页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
4. 【跨学科】爸爸告诉小东:“距地面越高,温度越低”,并给小东出示了下面的表格:
|距地面的高度 $ h/km $| $ 0 $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | $ 5 $ |
|温度 $ T/^{\circ}C $| $ 20 $ | $ 14 $ | $ 8 $ | $ 2 $ | $ -4 $ | $ -10 $ |
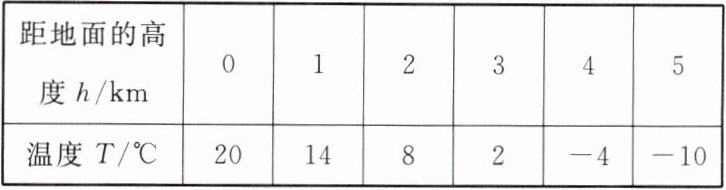
根据上表,请解答下面的问题:
(1)如果用 $ h $ 表示距地面的高度,用 $ T $ 表示温度,那么随着 $ h $ 的变化,$ T $ 是如何变化的?
(2)你能写出 $ T $ 与 $ h $ 之间的关系式吗?
(3)$ T $ 是 $ h $ 的函数吗?请说明理由。
|距地面的高度 $ h/km $| $ 0 $ | $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | $ 5 $ |
|温度 $ T/^{\circ}C $| $ 20 $ | $ 14 $ | $ 8 $ | $ 2 $ | $ -4 $ | $ -10 $ |

根据上表,请解答下面的问题:
(1)如果用 $ h $ 表示距地面的高度,用 $ T $ 表示温度,那么随着 $ h $ 的变化,$ T $ 是如何变化的?
(2)你能写出 $ T $ 与 $ h $ 之间的关系式吗?
(3)$ T $ 是 $ h $ 的函数吗?请说明理由。
答案:
解:
(1)由题表可知,高度h每上升1 km,温度T就下降6°C。
(2)T=20-6h。
(3)T是h的函数。理由如下:因为对于h的每一个取值,T都有唯一确定的值与它对应,所以T是h的函数。
(1)由题表可知,高度h每上升1 km,温度T就下降6°C。
(2)T=20-6h。
(3)T是h的函数。理由如下:因为对于h的每一个取值,T都有唯一确定的值与它对应,所以T是h的函数。
1. 给出下列变量之间的关系:①正方形的周长与边长;②圆的面积与半径;③三角形的面积与底边长;④商场中某种商品的单价为 $ a $ 元,销售总额与销售数量。具有函数关系的共有(
A.$ 2 $ 个
B.$ 3 $ 个
C.$ 4 $ 个
D.$ 1 $ 个
B
)。A.$ 2 $ 个
B.$ 3 $ 个
C.$ 4 $ 个
D.$ 1 $ 个
答案:
B
2. 下列关系中变量 $ y $ 不是变量 $ x $ 的函数的是(
A.$ y = x + 1 $
B.$ y = \dfrac{1}{x} $
C.$ y = -2x $
D.$ |y| = x $
D
)。A.$ y = x + 1 $
B.$ y = \dfrac{1}{x} $
C.$ y = -2x $
D.$ |y| = x $
答案:
D
3. 如图所示的是用 $ 10 $ 根火柴棒摆出的 $ 3 $ 个正方形的图案,当火柴棒的根数 $ m $ 变化时,所摆出的正方形个数 $ n $ 也随之变化。对于这一变化过程,下列说法不正确的是(
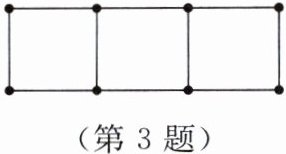
A.$ m $,$ n $ 都是变量
B.$ n $ 是自变量,$ m $ 是因变量
C.$ m $ 是 $ n $ 的函数
D.$ n $ 是 $ m $ 的函数
D
)。
A.$ m $,$ n $ 都是变量
B.$ n $ 是自变量,$ m $ 是因变量
C.$ m $ 是 $ n $ 的函数
D.$ n $ 是 $ m $ 的函数
答案:
D
4. 下图是一个运算程序,若输入 $ x $ 的值为 $ 3 $,则输出 $ y $ 的值为

2
。
答案:
2
5. 某汽车油箱余油量 $ Q $(单位:$ L $)与汽车行驶路程 $ s $(单位:$ km $)有如下关系:
|行驶路程 $ s/km $| $ 0 $ | $ 20 $ | $ 40 $ | $ 60 $ | $ 80 $ | …$ $ |
|余油量 $ Q/L $| $ 40 $ | $ 38 $ | $ 36 $ | $ 34 $ | $ 32 $ | …$ $ |

该汽车每千米耗油量为 ______ $ L $。
|行驶路程 $ s/km $| $ 0 $ | $ 20 $ | $ 40 $ | $ 60 $ | $ 80 $ | …$ $ |
|余油量 $ Q/L $| $ 40 $ | $ 38 $ | $ 36 $ | $ 34 $ | $ 32 $ | …$ $ |

该汽车每千米耗油量为 ______ $ L $。
0.1
答案:
0.1
6. 已知两个变量 $ x $,$ y $ 满足关系式 $ 2x - 3y + 1 = 0 $。
(1)$ y $ 是 $ x $ 的函数吗?为什么?
(2)$ x $ 是 $ y $ 的函数吗?为什么?
(1)$ y $ 是 $ x $ 的函数吗?为什么?
(2)$ x $ 是 $ y $ 的函数吗?为什么?
答案:
解:
(1)由2x-3y+1=0,得y=$\frac{2x+1}{3}$。
因为对于x的每一个取值,y都有唯一确定的值与之对应,所以y是x的函数。
(2)由2x-3y+1=0,得x=$\frac{3y-1}{2}$。
因为对于y的每一个取值,x都有唯一确定的值与之对应,所以x是y的函数。
(1)由2x-3y+1=0,得y=$\frac{2x+1}{3}$。
因为对于x的每一个取值,y都有唯一确定的值与之对应,所以y是x的函数。
(2)由2x-3y+1=0,得x=$\frac{3y-1}{2}$。
因为对于y的每一个取值,x都有唯一确定的值与之对应,所以x是y的函数。
查看更多完整答案,请扫码查看


