第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
7. 下面的三个变化过程都涉及两个变量:
①汽车从 $ A $ 地匀速行驶到 $ B $ 地,汽车的剩余路程 $ y $ 与行驶时间 $ x $;
②将水箱中的水匀速放出,直至放完,水箱中的剩余水量 $ y $ 与放水时间 $ x $;
③用长度一定的绳子围成一个矩形,矩形的面积 $ y $ 与一边长 $ x $。
其中,变量 $ y $ 与变量 $ x $ 之间的函数关系能用下面的图象表示的是(
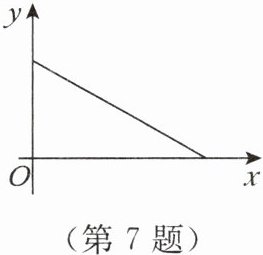
A.①②
B.①③
C.②③
D.①②③
①汽车从 $ A $ 地匀速行驶到 $ B $ 地,汽车的剩余路程 $ y $ 与行驶时间 $ x $;
②将水箱中的水匀速放出,直至放完,水箱中的剩余水量 $ y $ 与放水时间 $ x $;
③用长度一定的绳子围成一个矩形,矩形的面积 $ y $ 与一边长 $ x $。
其中,变量 $ y $ 与变量 $ x $ 之间的函数关系能用下面的图象表示的是(
A
)。
A.①②
B.①③
C.②③
D.①②③
答案:
A
8. 某电影院的一部分座位被排列成扇形,相应排数与座位数的关系如下表:
|排数| $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | …$ $ |
|座位数| $ 60 $ | $ 64 $ | $ 68 $ | $ 72 $ | …$ $ |
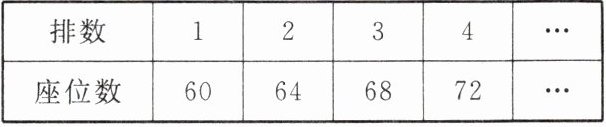
(1)上述哪些量在变化?自变量和因变量分别是什么?
(2)第 $ 5 $ 排、第 $ 6 $ 排各有多少个座位?
(3)第 $ n $ 排有多少个座位?
(4)若某排有 $ 136 $ 个座位,则它是第几排?
|排数| $ 1 $ | $ 2 $ | $ 3 $ | $ 4 $ | …$ $ |
|座位数| $ 60 $ | $ 64 $ | $ 68 $ | $ 72 $ | …$ $ |

(1)上述哪些量在变化?自变量和因变量分别是什么?
(2)第 $ 5 $ 排、第 $ 6 $ 排各有多少个座位?
(3)第 $ n $ 排有多少个座位?
(4)若某排有 $ 136 $ 个座位,则它是第几排?
答案:
解:
(1)排数与座位数在变化,其中自变量是排数,因变量是座位数。
(2)第5排有76个座位,第6排有80个座位。
(3)因为第1排有60座,即60+4×(1-1);第2排有64座,即60+4×(2-1);第3排有68座,即60+4×(3-1);…;第n排有60+4×(n-1)座,化简得:第n排有(4n+56)个座位。
(4)因为第n排有(4n+56)个座位,
所以4n+56=136。解得n=20。
(1)排数与座位数在变化,其中自变量是排数,因变量是座位数。
(2)第5排有76个座位,第6排有80个座位。
(3)因为第1排有60座,即60+4×(1-1);第2排有64座,即60+4×(2-1);第3排有68座,即60+4×(3-1);…;第n排有60+4×(n-1)座,化简得:第n排有(4n+56)个座位。
(4)因为第n排有(4n+56)个座位,
所以4n+56=136。解得n=20。
9. 【跨学科】声音在空气中传播的速度(简称“声速”)和气温的关系如下表:
|气温 $ /^{\circ}C $| $ 0 $ | $ 5 $ | $ 10 $ | $ 15 $ | $ 20 $ |
|声速 $ /(m/s) $| $ 331 $ | $ 334 $ | $ 337 $ | $ 340 $ | $ 343 $ |

(1)上表反映了
(2)若用 $ T(^{\circ}C) $ 表示气温,$ v(m/s) $ 表示声速,则随着 $ T $ 的增大 $ v $ 将发生怎样的变化?
(3)根据表中数据的对应关系,你发现这两个变量之间有什么规律?写出 $ v $ 与 $ T $ 之间的函数表达式。
(4)运用你发现的规律,解决问题:在气温为 $ 30^{\circ}C $ 发生闪电的夏夜,小明在看到闪电 $ 6 s $ 后才听到雷声,发生打雷的地方距小明大约有多远?
把T=30代入v=331+$\frac{3}{5}$T,得v=349。
349×6=2094(m)。
所以发生打雷的地方距小明大约有2094 m。
|气温 $ /^{\circ}C $| $ 0 $ | $ 5 $ | $ 10 $ | $ 15 $ | $ 20 $ |
|声速 $ /(m/s) $| $ 331 $ | $ 334 $ | $ 337 $ | $ 340 $ | $ 343 $ |

(1)上表反映了
声速与温度
之间的关系,其中温度
是自变量,声速
是温度
的函数。(2)若用 $ T(^{\circ}C) $ 表示气温,$ v(m/s) $ 表示声速,则随着 $ T $ 的增大 $ v $ 将发生怎样的变化?
随着T的增大,v也逐渐增大。
(3)根据表中数据的对应关系,你发现这两个变量之间有什么规律?写出 $ v $ 与 $ T $ 之间的函数表达式。
T每增加5°C,v就增加3 m/s,即T每增加1°C,v就增加$\frac{3}{5}$m/s,所以v=331+$\frac{3}{5}$T。
(4)运用你发现的规律,解决问题:在气温为 $ 30^{\circ}C $ 发生闪电的夏夜,小明在看到闪电 $ 6 s $ 后才听到雷声,发生打雷的地方距小明大约有多远?
把T=30代入v=331+$\frac{3}{5}$T,得v=349。
349×6=2094(m)。
所以发生打雷的地方距小明大约有2094 m。
答案:
解:
(1)声速与温度,温度,声速,温度。
(2)随着T的增大,v也逐渐增大。
(3)T每增加5°C,v就增加3 m/s,即T每增加1°C,v就增加$\frac{3}{5}$m/s,所以v=331+$\frac{3}{5}$T。
(4)把T=30代入v=331+$\frac{3}{5}$T,得v=349。
349×6=2094(m)。
所以发生打雷的地方距小明大约有2094 m。
(1)声速与温度,温度,声速,温度。
(2)随着T的增大,v也逐渐增大。
(3)T每增加5°C,v就增加3 m/s,即T每增加1°C,v就增加$\frac{3}{5}$m/s,所以v=331+$\frac{3}{5}$T。
(4)把T=30代入v=331+$\frac{3}{5}$T,得v=349。
349×6=2094(m)。
所以发生打雷的地方距小明大约有2094 m。
查看更多完整答案,请扫码查看


