《2025年智慧学习明天出版社七年级数学上册人教版》

1. 计算$0-2+10-7-5$的结果是(B)
A.0
B.-4
C.6
D.-6

答案： B

2. 把$(-6)-(-3)+(-2)-(+6)-(-7)$写成省略括号的和的形式是-6+3-2-6+7,读作略或略.

答案： -6+3-2-6+7;略;略

3. 计算(+16)+(-25)+(+24)+(-32)= [(+16)+(+24)]+[(-25)+(-32)]= (+40)+(-57)= -17. 从中可知,先把正数和正数、负数和负数分别结合在一起相加,计算比较简单.

答案： (+16)；(+24)；(-25)；(-32)；-17；正；正；负；负

4. 上午10时气温是$5^{\circ}C$,晚上10时气温比上午低$-2^{\circ}C$,凌晨2时气温又比晚上高$-3^{\circ}C$,那么凌晨2时气温是多少?

答案： 4

5. 计算：
(1)$10-8-(-6)-(+4)$；
(2)$(-32)-(-27)-(-72)$；
(3)$[(-5)-(+8)]-(-3)$.

答案： 1. （1）
解：
$10 - 8 - (-6)-(+4)$
$=10 - 8 + 6 - 4$
$=(10 + 6)-(8 + 4)$
$=16 - 12$
$=4$
2. （2）
解：
$(-32)-(-27)-(-72)$
$=-32 + 27+72$
$=-32+(27 + 72)$
$=-32 + 99$
$=67$
3. （3）
解：
$[(-5)-(+8)]-(-3)$
$=(-5 - 8)+3$
$=-13 + 3$
$=-10$
综上，答案依次为：（1）$4$；（2）$67$；（3）$-10$。

6. 请判断下列计算过程是否正确? 若不正确,请说明从哪一步开始出现错误及出现错误的原因,并给出正确的解答过程.

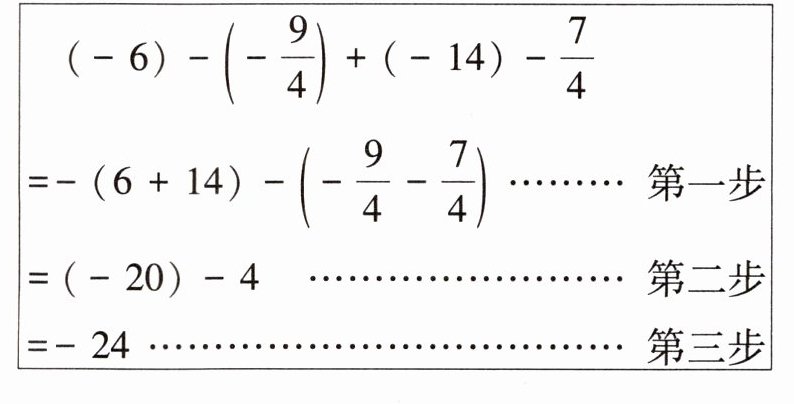
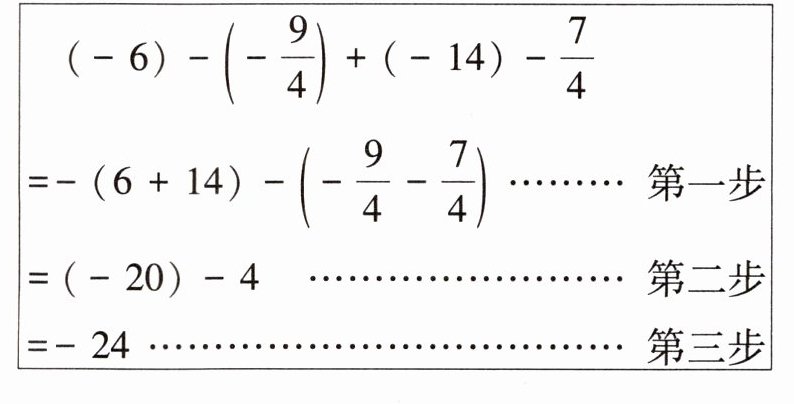
答案： 1. 首先判断原计算过程：
原计算过程**不正确**，从第一步开始出现错误。
错误原因：去括号法则使用错误，$-(-\frac{9}{4})-\frac{7}{4}=\frac{9}{4}-\frac{7}{4}$，而不是$-(-\frac{9}{4}-\frac{7}{4})$。
2. 然后给出正确的解答过程：
解：
对于$(-6)-(-\frac{9}{4})+(-14)-\frac{7}{4}$，
根据有理数的加减法法则，将式子变形为$[(-6)+(-14)]+(\frac{9}{4}-\frac{7}{4})$。
先计算括号内的式子：
计算$(-6)+(-14)$，根据同号两数相加，取相同的符号，并把绝对值相加，$(-6)+(-14)=-(6 + 14)=-20$；
计算$\frac{9}{4}-\frac{7}{4}$，根据同分母分数相减，分母不变，分子相减，$\frac{9}{4}-\frac{7}{4}=\frac{9 - 7}{4}=\frac{2}{4}=\frac{1}{2}$。
再计算$-20+\frac{1}{2}$，根据异号两数相加，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值，$-20+\frac{1}{2}=-(20-\frac{1}{2})=-19\frac{1}{2}$。
所以原计算从第一步开始错误，正确结果是$-19\frac{1}{2}$。

学习盘点
怎样进行有理数的加减混合运算? 在运用加法交换律和结合律时,应注意什么?

答案： 有理数加减混合运算步骤：1. 将减法转化为加法，即减去一个数等于加上这个数的相反数；2. 运用加法交换律和结合律进行简便运算。运用加法交换律和结合律时应注意：交换加数位置时，要连同前面的符号一起交换；结合时，通常把互为相反数的数、同号的数、能凑整的数结合在一起。

1. 计算$5-3+7-9+12= (5+7+12)+(-3-9)$时应用了(D)
A.加法交换律
B.加法结合律
C.分配律
D.加法交换律与加法结合律

答案： D