《2025年智慧学习明天出版社七年级数学上册人教版》

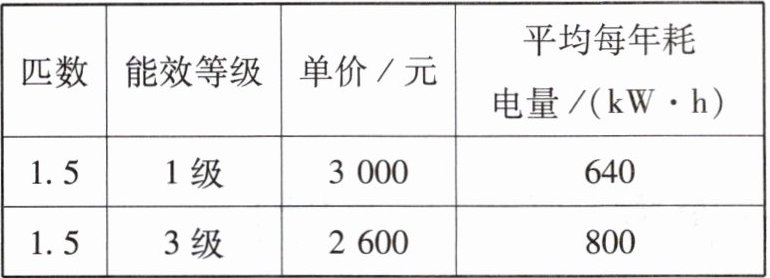
购买空调时,需要综合考虑空调的价格和耗电情况.某人打算从当年生产的两款空调中选购一台,下表是这两款空调的部分基本信息.如果电价是0.5元/(kW·h),请你分析他购买、使用哪款空调综合费用较低.
| 

答案： 1. 首先计算两款空调使用$n$年的总费用公式：
设使用$n$年，对于$1$级能效空调，总费用$y_1$（元）由单价和$n$年的电费组成。
已知单价为$3000$元，平均每年耗电量为$640kW· h$，电价是$0.5$元$/(kW· h)$，根据“总费用$=$空调单价$+$电费”，电费$=$每年耗电量$×$电价$×$使用年数，所以$y_1 = 3000+0.5×640n$。
化简$y_1$：$y_1 = 3000 + 320n$。
对于$3$级能效空调，总费用$y_2$（元），单价为$2600$元，平均每年耗电量为$800kW· h$，同理可得$y_2=2600 + 0.5×800n$。
化简$y_2$：$y_2=2600 + 400n$。
2. 然后求两款空调总费用相等时的使用年数$n$：
令$y_1=y_2$，即$3000 + 320n=2600 + 400n$。
移项可得：$400n-320n=3000 - 2600$。
合并同类项：$80n = 400$。
解得$n = 5$。
3. 接着分析$n$不同取值时$y_1$与$y_2$的大小关系：
当$n\lt5$时：
$y_1-y_2=(3000 + 320n)-(2600 + 400n)=3000 + 320n-2600 - 400n=400 - 80n$。
因为$n\lt5$，所以$80n\lt400$，$400 - 80n\gt0$，即$y_1\gt y_2$。
当$n = 5$时，$y_1=y_2$。
当$n\gt5$时：
$y_1 - y_2=400 - 80n$，因为$n\gt5$，所以$80n\gt400$，$400 - 80n\lt0$，即$y_1\lt y_2$。
解：设使用$n$年，$1$级能效空调总费用$y_1 = 3000+0.5×640n=3000 + 320n$，$3$级能效空调总费用$y_2=2600 + 0.5×800n=2600 + 400n$。
令$y_1=y_2$，即$3000 + 320n=2600 + 400n$，解得$n = 5$。
当$n\lt5$时，$y_1\gt y_2$；当$n = 5$时，$y_1=y_2$；当$n\gt5$时，$y_1\lt y_2$。
所以，若使用年限小于$5$年，购买$3$级能效空调综合费用低；若使用年限等于$5$年，购买两款空调综合费用一样；若使用年限大于$5$年，购买$1$级能效空调综合费用低。

某园林的门票每张80元,一次性使用.考虑到人们的不同需求,也为了吸引更多的游客,该园林除保留原来的售票方法外,还推出了一种“购买个人年票”的方法.个人年票从购票日起,可供持票者使用一年.年票每张60元,入园时需买一张2元的门票.
(1) 如果你计划一年中在该园林的门票上花100元,应选择哪一种购票方式?
(2) 在什么情况下购买年票与不购买年票花费相等?
(3) 你认为在什么情况下购买年票比较合算?

答案： $(1)$ 分析两种购票方式可入园次数
设不购买年票可入园$x$次，购买年票可入园$y$次。
不购买年票：
已知门票每张$80$元，计划花$100$元，根据公式$总价 = 单价×数量$，可得$80x = 100$，解得$x=\frac{100}{80}=1.25$（次），因为次数只能为整数，所以不购买年票最多入园$1$次。
购买年票：
年票每张$60$元，入园时需买一张$2$元的门票，计划花$100$元，则$60 + 2y = 100$，移项可得$2y=100 - 60$，即$2y = 40$，解得$y = 20$（次）。
因为$20＞1$，所以应选择购买年票的购票方式。
$(2)$ 计算购买年票与不购买年票花费相等时的入园次数
设入园$m$次时，购买年票与不购买年票花费相等。
不购买年票花费为$80m$元，购买年票花费为$(60 + 2m)$元，可列方程：
$80m=60 + 2m$
移项：$80m-2m=60$，即$78m = 60$，解得$m=\frac{60}{78}=\frac{10}{13}\approx 30$（次）。
$(3)$ 分析购买年票比较合算的情况
设入园$n$次。
购买年票花费$60 + 2n$元，不购买年票花费$80n$元，当购买年票合算时，$60 + 2n＜80n$。
移项可得：$60＜80n - 2n$，即$60＜78n$，解得$n ＞ \frac{60}{78}=\frac{10}{13}\approx30$（次）。
所以当入园次数大于$30$次时，购买年票比较合算。
综上，答案依次为：$(1)$ 应选择**购买年票**的购票方式；$(2)$ 入园$\boldsymbol{30}$次时，购买年票与不购买年票花费相等；$(3)$ 入园次数**大于$\boldsymbol{30}$次**时，购买年票比较合算 。

学习盘点
列方程解应用题的关键是什么? 怎样才能列出符合实际的方程?

答案： 列方程解应用题的关键是找出等量关系；通过审题、设未知数、依据等量关系列方程并检验解的实际意义可列出符合实际的方程。

1. 某校七年级三个班级联合开展户外研学活动,此次活动由一班班长负责购买车票,票价每张20元.有两种优惠方案:

班长思考一会儿说,无论选择哪种方案所要付的车费是一样的,则七年级三个班级共有(D)
A.60人
B.61人
C.62人
D.63人

答案： D