《2025年智慧学习明天出版社七年级数学上册人教版》

1. 先化简,再求值：
$ \frac{1}{3}a - \left(\frac{1}{2}a - 4b - 6c\right) + 3(-2c + 2b), $
其中$ a = -12, b = \frac{1}{5}, c = 2024. $

答案： 化简为$-\dfrac{1}{6}a+10b$.当$a=-12$,$b=\dfrac{1}{5}$,$c=2024$时,原式$=4$.

2. 如图,池塘边有一块长为20m,宽为10m的长方形土地,现在将其余三面留出宽都是xm的小路,中间余下的长方形部分作为菜地,用代数式表示：
(1) 菜地的长$ a = $20 - 2xm,宽$ b = $10 - xm；菜地的周长$ l = $60 - 6xm；
(2)$ x = 1 $时,求菜地的周长.
54m

答案： 1. （1）
对于菜地的长a：
已知长方形土地长为20m，其余三面留出宽都是xm的小路，那么菜地的长a=(20 - 2x)m；
对于菜地的宽b：已知长方形土地宽为10m，留出宽为xm的小路，所以菜地的宽b=(10 - x)m。
对于菜地的周长l：
根据长方形周长公式l = 2×( )长+宽)，把a=(20 - 2x)，b=(10 - x)代入可得： - l = 2[(20 - 2x)+(10 - x)]。 - 先去括号：l = 2(20 - 2x + 10 - x)。 - 再合并同类项：l = 2(30 - 3x)。 - 最后根据乘法分配律a(b + c)=ab+ac，这里a = 2，b = 30，c=-3x，则l=(60 - 6x)m。2. （2） - 当x = 1时： - 把x = 1代入l = 60-6x中。 - 解：l=60 - 6×1。 - 根据先乘除后加减的运算顺序，先计算乘法：6×1 = 6。 - 再计算减法：l=60 - 6=54(m)。综上，（1）a=(20 - 2x)，b=(10 - x)，l=(60 - 6x)；（2）54m。

学习盘点
在求多项式的值的运算中,怎样计算更简单些？

答案： 先合并同类项化简多项式，再代入数值计算更简单。

1. 一个正方形的边长为acm,把它的边长增加2cm,得到的新正方形的周长是$(4a+8)$ cm.

答案： $(4a+8)$ cm

2. 如图,一块正方形铁皮的边长为$ x cm(x ＞ 4) $,如果一边截去宽4cm的一条,另一边截去宽3cm的一条,求剩余部分(阴影)的周长.

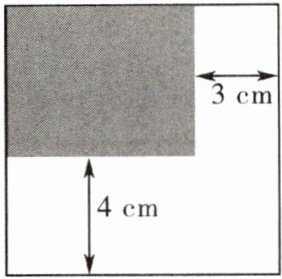
答案： $(4x-14)$ cm

3. 先化简下式,再求值：
$ (ab^{2} + 3a^{2}b) - 5(3a^{2}b - ab^{2}) $,其中$ a = \frac{1}{2}, b = \frac{1}{3}. $

答案： 化简为$6ab^{2}-12a^{2}b$.当$a=\dfrac{1}{2}$,$b=\dfrac{1}{3}$时,原式$=-\dfrac{2}{3}$.

4. 一列和谐号动车组火车行驶在京广铁路线上,动车从北京出发时车上有$ (5a - 2b) $个人,到石家庄站下去了一半人,但又上车若干人,这时车上有$ (10a - 3b) $人.
(1) 中途上车多少人？
(2) 当$ a = 50, b = 40 $时,中途上车多少人？

答案： $(1)$ 求中途上车的人数
解：
- 首先，计算到石家庄站下去一半人后车上剩余的人数：
已知出发时车上有$(5a - 2b)$人，下去一半人后，剩余人数为$\frac{1}{2}(5a - 2b)=\frac{5}{2}a - b$人。
- 然后，设中途上车$x$人，根据此时车上有$(10a - 3b)$人，可列方程：
$\frac{5}{2}a - b+x = 10a - 3b$。
- 最后，求解$x$：
移项可得$x=(10a - 3b)-(\frac{5}{2}a - b)$，
去括号得$x = 10a - 3b-\frac{5}{2}a + b$，
合并同类项得$x=(10a-\frac{5}{2}a)+(-3b + b)=\frac{15}{2}a - 2b$。
所以中途上车$(\frac{15}{2}a - 2b)$人。
$(2)$ 当$a = 50$，$b = 40$时，求中途上车的人数
解：
把$a = 50$，$b = 40$代入$\frac{15}{2}a - 2b$得：
$\frac{15}{2}×50 - 2×40$
$=15×25 - 80$
$=375 - 80$
$= 295$（人）
所以当$a = 50$，$b = 40$时，中途上车$295$人。
综上，答案依次为：$(1)$$\boldsymbol{(\frac{15}{2}a - 2b)}$人；$(2)$$\boldsymbol{295}$人。