《2025年名校课堂八年级数学上册人教版云南专版》

10. 对任意整数$n$，按下列程序计算，则输出结果为(D)
$\boxed{输入n}\to\boxed{平方}\to\boxed{+n}\to\boxed{÷ n}\to\boxed{-n}\to\boxed{输出结果}$

A.$n$
B.$n^{2}$
C.$2n$
D.$1$

答案： 10.D

11. 已知$A = 2x$，$B$是多项式，在计算$B÷ A$时，小强同学把$B÷ A$误看成了$B + A$，结果得到$2x^{2}-x$，则$B÷ A$正确的结果是(D)

A.$2x^{2}+x$
B.$2x^{2}-3x$
C.$x+\frac{1}{2}$
D.$x-\frac{3}{2}$

答案： 11.D

12. 长方形的面积为$4a^{2}-6ab + 2a$，若它的一条边长为$2a$，则它的周长是8a - 6b + 2.

答案： 12.8a - 6b + 2

13. 计算：$(2x^{n + 2}-4x^{n + 1}+2x^{n})÷(-6x^{n})=$-1/3x² + 2/3x - 1/3.

答案： 13.-1/3x² + 2/3x - 1/3

14. 计算：
（1）$(\frac{1}{3}a^{2}b^{2}-2ab^{2}-b^{3})÷(-2b)^{2}$；
（2）$[2a^{2}\cdot8a^{2}+(2a)^{3}-4a^{2}]÷(2a)$.

答案： 14.
(1)解：原式 = (1/3a²b² - 2ab² - b³) ÷ (4b²) = 1/12a² - 1/2a - 1/4b.
(2)解：原式 = (16a⁴ + 8a³ - 4a²) ÷ (2a) = 8a³ + 4a² - 2a.

15. 先化简，再求值：
（1）$(5x^{2}y^{3}-4x^{3}y^{2}+6x)÷(6x)$，其中$x = - 2$，$y = 2$；
（2）A|华师二附中校本经典题$[(2a + b)(2a - b)-(2a - b)^{2}]÷(2a - b)$，其中$a = 1$，$b = 2$.

答案： 15.
(1)解：原式 = 5/6xy³ - 2/3x²y² + 1. 当x = -2,y = 2时，原式 = 5/6 ×(-2) × 8 - 2/3 × 4 × 4 + 1 = -23.
(2)解：原式 = (2a + b)(2a - b) ÷ (2a -b) - (2a - b)² ÷ (2a - b) = 2a + b - (2a - b) = 2b. 当b = 2时，原式 = 4.

16. A|华师二附

中

校本经典题 已知多项式$A$与单项式$5xy^{2}$的差，除以$(xy)$，所得的商是$3x + y$，求$A$.

答案： 16.解：由题意，得(A - 5xy²) ÷ (xy) = 3x + y，
∴A - 5xy² = xy(3x + y).
∴A = xy(3x + y) + 5xy² = 3x²y + xy² + 5xy² = 3x²y + 6xy².

17. A|北师大附属实验校本经典题 如图 1 所示的瓶子中盛满水，如果将这个瓶子中的水全部倒入图 2 的杯子中，那么你知道一共需要多少个这样的杯子吗？（单位：cm）

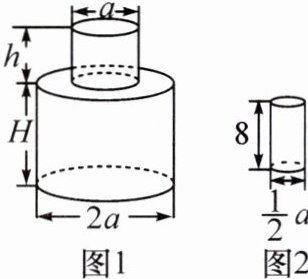
答案： 17.解：[π(-1/2a)²h + π(1/2 × 2a)²H] ÷ [π(1/2 × 1/2a)² × 8] = (1/4πa²h + πa²H) ÷ (1/2πa²) = (-1/2h + 2H)个. 答：一共需要(-1/2h + 2H)个这样的杯子.