第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 【教材母题变式】(教材 P85 习题 T11 变式)
如图,点 C 是线段 AB 上除点 A,B 外的任意一点,分别以 AC,BC 为边在线段 AB 的同侧作等边三角形 ACD 和等边三角形 BCE,连接 AE 交 DC 于点 M,连接 BD 交 CE 于点 N,连接 MN. 求证:
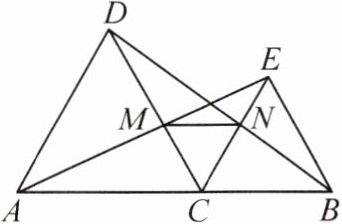
(1) $ AE = BD $;
(2) $ MN // AB $.
【拓展设问】 若 BD 与 AE 相交于点 P,连接 CP,判断下列结论是否正确,对的打“√”,错的打“×”.
(1) $ \angle APD = 60^{\circ} $;(
(2) $ \triangle ACM \cong \triangle DCN $;(
(3) $ CM = CN $;(
(4) $ \triangle CMN $是等边三角形;(
(5) $ ME = BE $;(
(6) PC 平分 $ \angle APB $. (
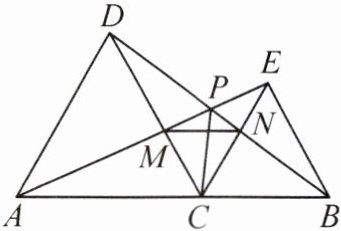
如图,点 C 是线段 AB 上除点 A,B 外的任意一点,分别以 AC,BC 为边在线段 AB 的同侧作等边三角形 ACD 和等边三角形 BCE,连接 AE 交 DC 于点 M,连接 BD 交 CE 于点 N,连接 MN. 求证:

(1) $ AE = BD $;
(2) $ MN // AB $.
【拓展设问】 若 BD 与 AE 相交于点 P,连接 CP,判断下列结论是否正确,对的打“√”,错的打“×”.
(1) $ \angle APD = 60^{\circ} $;(
√
)(2) $ \triangle ACM \cong \triangle DCN $;(
√
)(3) $ CM = CN $;(
√
)(4) $ \triangle CMN $是等边三角形;(
√
)(5) $ ME = BE $;(
×
)(6) PC 平分 $ \angle APB $. (
√
)
答案:
1.证明:
(1)
∵△ACD 和△BCE 是等边三角形,
∴AC = DC,CE = CB, ∠DCA = ∠ECB = 60°.
∴∠DCA + ∠DCE = ∠ECB + ∠DCE,即∠ACE = ∠DCB. 在△ACE 和△DCB 中,$\begin{cases} ∠ACE = ∠DCB \\ AC = DC \\ CE = CB \end{cases},$
∴△ACE ≌ △DCB(SAS).
∴AE = BD.
(2)
∵△ACE ≌ △DCB,
∴∠CAE = ∠CDB.
∵∠ACD = ∠ECB = 60°,且 A,C,B 三点共线,
∴∠DCN = 60°.
∴∠ACM = ∠DCN. 在△ACM 和△DCN 中,$\begin{cases} AC = DC \\ ∠MAC = ∠NDC \\ ∠ACM = ∠DCN \end{cases},$
∴△ACM ≌ △DCN(ASA).
∴MC = NC.
∵∠MCN = 60°,
∴△MCN 为等边三角形.
∴∠NMC = 60°.
∴∠NMC = ∠DCA.
∴MN//AB.
【拓展设问】
(1)√
(2)√
(3)√
(4)√
(5)×
(6)√
(1)
∵△ACD 和△BCE 是等边三角形,
∴AC = DC,CE = CB, ∠DCA = ∠ECB = 60°.
∴∠DCA + ∠DCE = ∠ECB + ∠DCE,即∠ACE = ∠DCB. 在△ACE 和△DCB 中,$\begin{cases} ∠ACE = ∠DCB \\ AC = DC \\ CE = CB \end{cases},$
∴△ACE ≌ △DCB(SAS).
∴AE = BD.
(2)
∵△ACE ≌ △DCB,
∴∠CAE = ∠CDB.
∵∠ACD = ∠ECB = 60°,且 A,C,B 三点共线,
∴∠DCN = 60°.
∴∠ACM = ∠DCN. 在△ACM 和△DCN 中,$\begin{cases} AC = DC \\ ∠MAC = ∠NDC \\ ∠ACM = ∠DCN \end{cases},$
∴△ACM ≌ △DCN(ASA).
∴MC = NC.
∵∠MCN = 60°,
∴△MCN 为等边三角形.
∴∠NMC = 60°.
∴∠NMC = ∠DCA.
∴MN//AB.
【拓展设问】
(1)√
(2)√
(3)√
(4)√
(5)×
(6)√
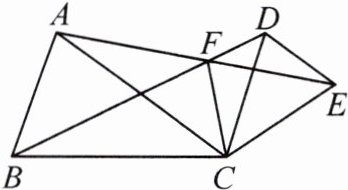
2. 如图,已知等腰三角形 ACB 和等腰三角形 DCE,$ AC = BC $,$ DC = EC $,$ \angle ACB = \angle DCE $,连接 BD,AE 交于点 F,连接 CF. 求证:
(1) $ AE = BD $;
(2) $ \angle AFB = \angle ACB $;
(3) FC 平分 $ \angle BFE $.
(1) $ AE = BD $;
(2) $ \angle AFB = \angle ACB $;
(3) FC 平分 $ \angle BFE $.

答案:
2.证明:
(1)
∵∠ACB = ∠DCE,
∴∠ACB + ∠ACD = ∠DCE + ∠ACD,即∠BCD = ∠ACE. 又
∵AC = BC,DC = EC,
∴△BCD ≌ △ACE(SAS).
∴AE = BD.
(2)设 AC,BD 相交于点 O.
∵△BCD ≌ △ACE,
∴∠CAE = ∠CBD. 又
∵∠AOF = ∠BOC,
∴∠AFB = ∠ACB.
(3)过点 C 分别作 CM ⊥ BD 于点 M,CN ⊥ EF 于点 N,则∠BMC = ∠ANC = 90°. 在△BCM 和△ACN 中,$\begin{cases} ∠BMC = ∠ANC \\ ∠CBM = ∠CAN \\ BC = AC \end{cases},$
∴△BCM ≌ △ACN(AAS).
∴CM = CN.
∴FC 平分∠BFE.
(1)
∵∠ACB = ∠DCE,
∴∠ACB + ∠ACD = ∠DCE + ∠ACD,即∠BCD = ∠ACE. 又
∵AC = BC,DC = EC,
∴△BCD ≌ △ACE(SAS).
∴AE = BD.
(2)设 AC,BD 相交于点 O.
∵△BCD ≌ △ACE,
∴∠CAE = ∠CBD. 又
∵∠AOF = ∠BOC,
∴∠AFB = ∠ACB.
(3)过点 C 分别作 CM ⊥ BD 于点 M,CN ⊥ EF 于点 N,则∠BMC = ∠ANC = 90°. 在△BCM 和△ACN 中,$\begin{cases} ∠BMC = ∠ANC \\ ∠CBM = ∠CAN \\ BC = AC \end{cases},$
∴△BCM ≌ △ACN(AAS).
∴CM = CN.
∴FC 平分∠BFE.
查看更多完整答案,请扫码查看


