第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 对于一个形状规则的匀质长方形薄板,其重心位置在(
A.长方形的任意一个顶点处
B.长方形两条对角线的交点处
C.长方形的一条边上
D.长方形的外部
B
)A.长方形的任意一个顶点处
B.长方形两条对角线的交点处
C.长方形的一条边上
D.长方形的外部
答案:
1.B
2. 如图所示的网格由边长相同的小正方形组成,点 $ A,B,C,D,E,F,G $ 在小正方形的格点上,则 $ \triangle ABC $ 的重心是(
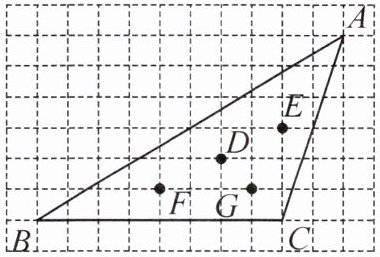
A.点 $ D $
B.点 $ E $
C.点 $ F $
D.点 $ G $
A
)
A.点 $ D $
B.点 $ E $
C.点 $ F $
D.点 $ G $
答案:
2.A
3. 发现与探究:三角形三条中线的交点叫三角形的重心. 重心是个物理名词. 从效果上看,我们可以认为物体所受重力的合力集中于一点,这一点叫物体的重心. 如图 1,如果取一块均匀的三角形纸板,用一根细线绳从重心 $ O $ 处将三角形提起来,纸板就会处于水平状态. 为什么会平衡呢?希望你经过下面的探索过程能得到答案.
如图 2,$ AD $ 是 $ \triangle ABC $ 的中线,$ \triangle ACD $ 与 $ \triangle ABD $ 等底等高,面积相等,记作 $ S_{\triangle ACD}=S_{\triangle ABD} $.
如图 3,若 $ \triangle ABC $ 的三条中线 $ AD,BE,CF $ 相交于点 $ G $,则 $ GD $ 是 $ \triangle GBC $ 的中线,利用上述结论可得 $ S_{\triangle GCD}=S_{\triangle GBD} $,同理 $ S_{\triangle GBF}=S_{\triangle GAF} $,$ S_{\triangle GAE}=S_{\triangle GCE} $.
(1) 如图 3,设 $ S_{\triangle GCD}=x $,$ S_{\triangle GBF}=y $,$ S_{\triangle GAE}=z $,猜想 $ x,y,z $ 之间的数量关系,并证明你的猜想.
(2) 由 (1) 可知,被三条中线分成的六个三角形面积
(3) 如图 4,$ \triangle ABC $ 的两条中线 $ BD,CE $ 相交于点 $ G $,点 $ G $ 是 $ \triangle ABC $ 的重心,$ BD=6 $,$ CE=9 $,$ BD \perp CE $,求四边形 $ AEGD $ 的面积.

如图 2,$ AD $ 是 $ \triangle ABC $ 的中线,$ \triangle ACD $ 与 $ \triangle ABD $ 等底等高,面积相等,记作 $ S_{\triangle ACD}=S_{\triangle ABD} $.
如图 3,若 $ \triangle ABC $ 的三条中线 $ AD,BE,CF $ 相交于点 $ G $,则 $ GD $ 是 $ \triangle GBC $ 的中线,利用上述结论可得 $ S_{\triangle GCD}=S_{\triangle GBD} $,同理 $ S_{\triangle GBF}=S_{\triangle GAF} $,$ S_{\triangle GAE}=S_{\triangle GCE} $.
(1) 如图 3,设 $ S_{\triangle GCD}=x $,$ S_{\triangle GBF}=y $,$ S_{\triangle GAE}=z $,猜想 $ x,y,z $ 之间的数量关系,并证明你的猜想.
(2) 由 (1) 可知,被三条中线分成的六个三角形面积
相等
. 如果 $ \triangle ABC $ 的面积为 $ m $,那么用含有 $ m $ 的式子表示 $ \triangle BGC $ 的面积为$\frac{1}{3}m$
,$ BG:GE= $$2:1$
.(3) 如图 4,$ \triangle ABC $ 的两条中线 $ BD,CE $ 相交于点 $ G $,点 $ G $ 是 $ \triangle ABC $ 的重心,$ BD=6 $,$ CE=9 $,$ BD \perp CE $,求四边形 $ AEGD $ 的面积.

答案:
3.解:
(1)猜想:$x = y = z$。证明:由题意可知,$S_{\triangle GCD} = S_{\triangle GBD} = x$,$S_{\triangle GBF} = S_{\triangle AGF} = y$,$S_{\triangle GAE} = S_{\triangle GCE} = z$,$\because S_{\triangle ABD} = S_{\triangle ACD}$,$\therefore 2y + x = 2z + x$。$\therefore y = z$。$\because S_{\triangle CBE} = S_{\triangle ABE}$,$\therefore 2x + z = 2y + z$。$\therefore x = y$。$\therefore x = y = z$。
(2)相等 $\frac{1}{3}m$
$2:1$
(3)$\because$点$G$是$\triangle ABC$的重心,$\therefore$由
(2)可知,$BG:GD = CG:GE =$
$2:1$。$\because BD = 6$,$CE = 9$,$\therefore BG = 4$,$CG = 6$。$\because BD\perp CE$,$\therefore S_{\triangle BGC} = \frac{1}{2}BG\cdot$
$CG = \frac{1}{2}×4×6 = 12$。由
(2)可知,$S_{\triangle ABC} = 3S_{\triangle BGC} = 36$,$S_{\triangle BEG} = S_{\triangle CDG} =$
$\frac{1}{2}S_{\triangle BGC} = 6$。$\therefore S_{四边形AEGD} = 36 - 6 - 6 - 12 = 12$。
3.解:
(1)猜想:$x = y = z$。证明:由题意可知,$S_{\triangle GCD} = S_{\triangle GBD} = x$,$S_{\triangle GBF} = S_{\triangle AGF} = y$,$S_{\triangle GAE} = S_{\triangle GCE} = z$,$\because S_{\triangle ABD} = S_{\triangle ACD}$,$\therefore 2y + x = 2z + x$。$\therefore y = z$。$\because S_{\triangle CBE} = S_{\triangle ABE}$,$\therefore 2x + z = 2y + z$。$\therefore x = y$。$\therefore x = y = z$。
(2)相等 $\frac{1}{3}m$
$2:1$
(3)$\because$点$G$是$\triangle ABC$的重心,$\therefore$由
(2)可知,$BG:GD = CG:GE =$
$2:1$。$\because BD = 6$,$CE = 9$,$\therefore BG = 4$,$CG = 6$。$\because BD\perp CE$,$\therefore S_{\triangle BGC} = \frac{1}{2}BG\cdot$
$CG = \frac{1}{2}×4×6 = 12$。由
(2)可知,$S_{\triangle ABC} = 3S_{\triangle BGC} = 36$,$S_{\triangle BEG} = S_{\triangle CDG} =$
$\frac{1}{2}S_{\triangle BGC} = 6$。$\therefore S_{四边形AEGD} = 36 - 6 - 6 - 12 = 12$。
查看更多完整答案,请扫码查看


