第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
【教材母题】(教材 P22 复习题 T8)如图,△ABC 的∠ABC 和∠ACB 的平分线 BE,CF 相交于点 G. 求证:
(1)∠BGC = 180° - $\frac{1}{2}$(∠ABC + ∠ACB);
(2)∠BGC = 90° + $\frac{1}{2}$∠A.

(1)∠BGC = 180° - $\frac{1}{2}$(∠ABC + ∠ACB);
(2)∠BGC = 90° + $\frac{1}{2}$∠A.

答案:
证明:$(1)$
∵$BE,$$CF$分别是$∠ABC,$$∠ACB$的平分线,
∴$∠GBC + ∠GCB = \frac{1}{2}(∠ABC + ∠ACB). $
∴$∠BGC = 180° - (∠GBC + ∠GCB). $
∴$∠BGC = 180° - \frac{1}{2}(∠ABC + ∠ACB). (2)$由$(1)$知$∠BGC = 180° - \frac{1}{2}(∠ABC + ∠ACB),$$∠ABC + ∠ACB = 180° - ∠A,$
∴$∠BGC = 180° - \frac{1}{2}(180° - ∠A). $
∴$∠BGC = 90° + \frac{1}{2}∠A.$
∵$BE,$$CF$分别是$∠ABC,$$∠ACB$的平分线,
∴$∠GBC + ∠GCB = \frac{1}{2}(∠ABC + ∠ACB). $
∴$∠BGC = 180° - (∠GBC + ∠GCB). $
∴$∠BGC = 180° - \frac{1}{2}(∠ABC + ∠ACB). (2)$由$(1)$知$∠BGC = 180° - \frac{1}{2}(∠ABC + ∠ACB),$$∠ABC + ∠ACB = 180° - ∠A,$
∴$∠BGC = 180° - \frac{1}{2}(180° - ∠A). $
∴$∠BGC = 90° + \frac{1}{2}∠A.$
1. (昭通昭阳区期中)如图,点 O 是△ABC 内一点,∠A = 60°,BO,CO 分别是∠ABC 和∠ACB 的平分线,则∠BOC 等于 (

A.110°
B.120°
C.130°
D.无法确定
B
)
A.110°
B.120°
C.130°
D.无法确定
答案:
1.B
2. (曲靖月考改编)如图,∠ACD 是△ABC 的外角,∠ABC 的平分线与∠ACD 的平分线交于点 A₁,∠A₁BC 的平分线与∠A₁CD 的平分线交于点 A₂,……,$∠A_{n - 1}BC $的平分线与$∠A_{n - 1}CD $的平分线交于点 A_n. 设∠A = θ.
(1)求∠A₁ 的度数;
(2)直接写出∠A_n 的度数.

(1)求∠A₁ 的度数;
(2)直接写出∠A_n 的度数.

答案:
2.
(1)
∵BA₁是∠ABC的平分线,CA₁是∠ACD的平分线,
∴$∠A₁BC = \frac{1}{2}∠ABC,$$∠A₁CD = \frac{1}{2}∠ACD. $又
∵∠ACD = ∠A + ∠ABC,∠A₁CD = ∠A₁BC + ∠A₁,
∴$\frac{1}{2}(∠A + ∠ABC) = \frac{1}{2}∠ABC + ∠A₁. $
∴$∠A₁ = \frac{1}{2}∠A. $
∵∠A = θ,
∴$∠A₁ = \frac{θ}{2}. (2)∠Aₙ = \frac{θ}{2^n}.$
(1)
∵BA₁是∠ABC的平分线,CA₁是∠ACD的平分线,
∴$∠A₁BC = \frac{1}{2}∠ABC,$$∠A₁CD = \frac{1}{2}∠ACD. $又
∵∠ACD = ∠A + ∠ABC,∠A₁CD = ∠A₁BC + ∠A₁,
∴$\frac{1}{2}(∠A + ∠ABC) = \frac{1}{2}∠ABC + ∠A₁. $
∴$∠A₁ = \frac{1}{2}∠A. $
∵∠A = θ,
∴$∠A₁ = \frac{θ}{2}. (2)∠Aₙ = \frac{θ}{2^n}.$
3. 如图所示,BO,CO 分别是△ABC 的外角平分线.
(1)若∠ABC = 40°,∠ACB = 60°,则∠BOC =
(2)若∠A = 60°,则∠BOC =
(3)试探索∠BOC 与∠A 之间的数量关系.
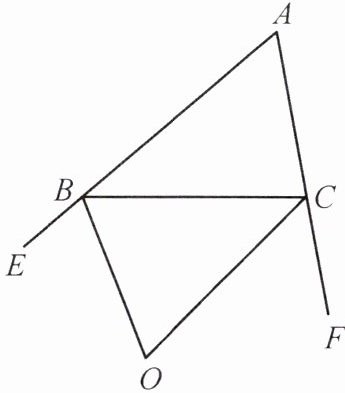
(1)若∠ABC = 40°,∠ACB = 60°,则∠BOC =
50°
;(2)若∠A = 60°,则∠BOC =
60°
;(3)试探索∠BOC 与∠A 之间的数量关系.

答案:
3.
(1)50°
(2)60°
(3)
∵BO,CO分别是△ABC的外角平分线,
∴$∠OBC = \frac{1}{2}∠EBC,$$∠OCB = \frac{1}{2}∠FCB.$在△BOC中,$∠BOC = 180° - (∠OBC + ∠OCB) = 180° - \frac{1}{2}(∠EBC + ∠FCB) = 180° - \frac{1}{2}(∠A + ∠ACB + ∠A + ∠ABC) = 180° - \frac{1}{2}(180° + ∠A) = 90° - \frac{1}{2}∠A.$
(1)50°
(2)60°
(3)
∵BO,CO分别是△ABC的外角平分线,
∴$∠OBC = \frac{1}{2}∠EBC,$$∠OCB = \frac{1}{2}∠FCB.$在△BOC中,$∠BOC = 180° - (∠OBC + ∠OCB) = 180° - \frac{1}{2}(∠EBC + ∠FCB) = 180° - \frac{1}{2}(∠A + ∠ACB + ∠A + ∠ABC) = 180° - \frac{1}{2}(180° + ∠A) = 90° - \frac{1}{2}∠A.$
查看更多完整答案,请扫码查看


