第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
8. (云南中考)已知△ABC是等腰三角形.若∠A=40°,则△ABC的顶角度数是
40°或100°
。
答案:
8.40°或100°
9. (本课时T8变式)若等腰三角形的一个角为100°,则另外两个角的度数分别为
40°,40°
。
答案:
9.40°,40°
10. (云南中考)如图,在等腰三角形ABC中,AB=AC,∠A=36°,BD⊥AC,则∠CBD=

18°
。
答案:
10.18°
11. (云南中考)已知AF是等腰三角形ABC底边BC上的高,若点F到直线AB的距离为3,则点F到直线AC的距离为(
A.$\frac{3}{2}$
B.2
C.3
D.$\frac{7}{2}$
C
)A.$\frac{3}{2}$
B.2
C.3
D.$\frac{7}{2}$
答案:
11.C
12. 新考向 传统文化 “廊桥凌水,楼阁傲天,状元故里状元桥,绶溪桥上看绶溪.”莆田绶溪公园开放“状元桥”和“状元阁”游览观光,其中“状元阁”的建筑风格堪称“咫尺之内再造乾坤”.如图,“状元阁”的顶端可看作等腰三角形ABC,AB=AC,D是边BC上的一点.下列条件不能说明AD是△ABC的角平分线的是(
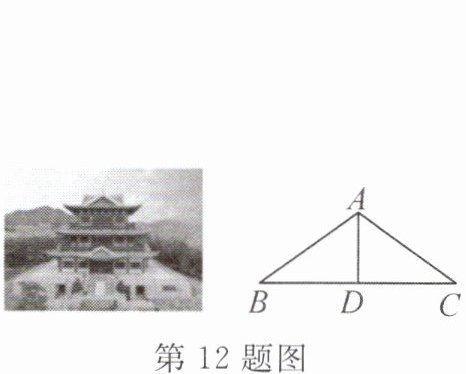
A.∠ADB=∠ADC
B.BD=CD
C.BC=2AD
D.$S_{△ABD}=S_{△ACD}$
C
)
A.∠ADB=∠ADC
B.BD=CD
C.BC=2AD
D.$S_{△ABD}=S_{△ACD}$
答案:
12.C
13. 新考向 真实情境 某平板电脑支架的示意图如图所示,其中AB=CD,EA=ED,为了使用的舒适性,可调整∠AEC的大小.若∠AEC增大16°,则∠BDE的变化情况是(
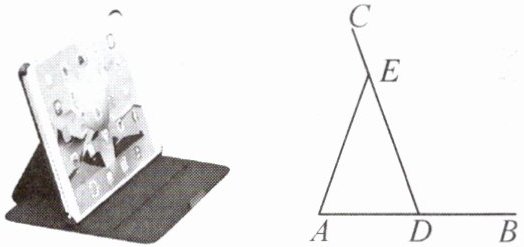
A.增大16°
B.减小16°
C.增大8°
D.减小8°
D
)
A.增大16°
B.减小16°
C.增大8°
D.减小8°
答案:
13.D
14. 如图,在△ABC中,∠ACB=90°,DE是AB的垂直平分线,∠CAE:∠EAB=4:1,求∠B的度数。


答案:
14.解:
∵DE是AB的垂直平分线,
∴AE = BE.
∴∠EAB = ∠B.
∵∠CAE∶∠EAB = 4∶1,
∴设∠EAB = x°, 则∠B = x°, ∠CAE = (4x)°.
∵∠ACB = 90°,
∴∠B + ∠CAE + ∠EAB = 90°.
∴x + 4x + x = 90, 解得x = 15.
∴∠B = 15°.
∵DE是AB的垂直平分线,
∴AE = BE.
∴∠EAB = ∠B.
∵∠CAE∶∠EAB = 4∶1,
∴设∠EAB = x°, 则∠B = x°, ∠CAE = (4x)°.
∵∠ACB = 90°,
∴∠B + ∠CAE + ∠EAB = 90°.
∴x + 4x + x = 90, 解得x = 15.
∴∠B = 15°.
15. 某数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两条射线之间,并使小棒两端分别在射线AB,AC上.
活动一:如图1所示,从点A₁开始,依次向右摆放小棒,使小棒在端点处互相垂直,A₁A₂为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?
答:
(2)设AA₁=A₁A₂=A₂A₃,θ=
活动二:如图2所示,从点A₁开始,用等长的小棒依次向右摆放,其中A₁A₂为第1根小棒,且A₁A₂=AA₁.
数学思考:
(3)若已经摆放了3根小棒,则θ₃=
(4)若只能摆放4根小棒,则θ的范围是

活动一:如图1所示,从点A₁开始,依次向右摆放小棒,使小棒在端点处互相垂直,A₁A₂为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?
答:
能
;(填“能”或“不能”)(2)设AA₁=A₁A₂=A₂A₃,θ=
22.5
°;活动二:如图2所示,从点A₁开始,用等长的小棒依次向右摆放,其中A₁A₂为第1根小棒,且A₁A₂=AA₁.
数学思考:
(3)若已经摆放了3根小棒,则θ₃=
4θ
;(用含θ的式子表示)(4)若只能摆放4根小棒,则θ的范围是
18°≤θ<22.5°
。
答案:
15.
(1)能
(2)22.5
(3)4θ
(4)18°≤θ<22.5°
(1)能
(2)22.5
(3)4θ
(4)18°≤θ<22.5°
查看更多完整答案,请扫码查看


