第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
5. (河北中考)如图,AD 与 BC 相交于点 O,△ABO 和△CDO 关于直线 PQ 对称,点 A,B 的对称点分别是点 C,D,则下列结论中不一定正确的是(
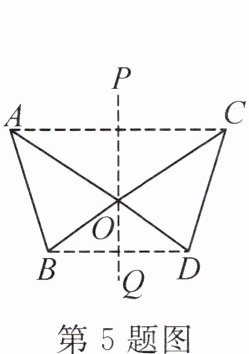
A.AD⊥BC
B.AC⊥PQ
C.△ABO≌△CDO
D.AC//BD
A
)
A.AD⊥BC
B.AC⊥PQ
C.△ABO≌△CDO
D.AC//BD
答案:
5.A
6. 如图,△ABC 与△A'B'C'关于直线 l 对称,∠A=50°,∠C'=30°,则∠B 的度数为
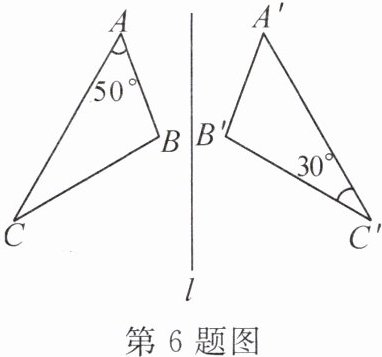
100°
.
答案:
6.100°
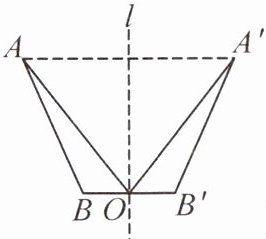
7. (教材 P65 新增练习 T3 变式)如图,线段 AB 与 A'B'关于直线 l 对称,BB'交直线 l 于点 O,连接 AO,A'O.
(1)AB=
(2)△OAB 与△OA'B'关于直线 l
(3)连接 AA',试判断 AA'与 BB'的位置关系,并说明理由.
(1)AB=
A′B′
,OA=OA′
,直线 l 垂直平分线段BB′
.(2)△OAB 与△OA'B'关于直线 l
成轴对称
,△OAB≌
△OA'B',∠ABO=∠A′B′O
,∠AOB'=∠A′OB
.(3)连接 AA',试判断 AA'与 BB'的位置关系,并说明理由.

答案:
7.解:
(1)A′B′ OA′ BB′
(2)成轴对称 ≌ A′B′O A′OB
(3)AA′ //BB′. 理由:
∵l⊥AA′,l⊥BB′,
∴AA′//BB′.
(1)A′B′ OA′ BB′
(2)成轴对称 ≌ A′B′O A′OB
(3)AA′ //BB′. 理由:
∵l⊥AA′,l⊥BB′,
∴AA′//BB′.
8. (哈尔滨中考)如图,在 Rt△ABC 中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为 D,△ADB 与△ADB'关于直线 AD 对称,点 B 的对称点是点 B',则∠CAB'的度数为(
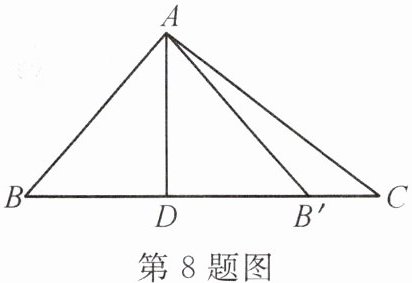
A.10°
B.20°
C.30°
D.40°
A
)
A.10°
B.20°
C.30°
D.40°
答案:
8.A
9. 如图,一种滑翔伞的形状是左右成轴对称的四边形 ABCD,其中∠BAD=150°,∠B=40°,则∠ACD 的度数是
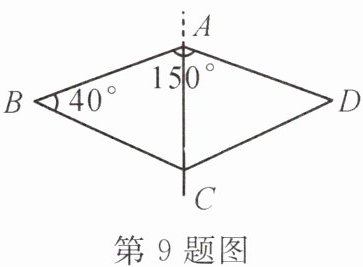
65°
.
答案:
9.65°
10. 如图,△ABC 是轴对称图形,且直线 AD 是△ABC 的对称轴,点 E,F 是线段 AD 上的任意两点.若△ABC 的面积为 12 cm²,求图中阴影部分的面积之和.
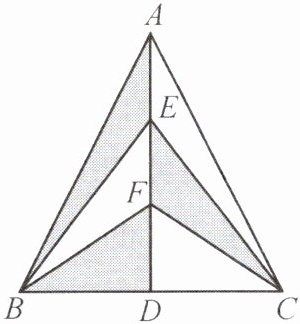

答案:
10.解:
∵△ABC是轴对称图形,且直线 AD 是对称轴,
∴△ABD与△ACD关于直线 AD 成轴对称.
∴$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2} × 12=6 (cm^2). $又
∵点 E,F 是 AD 上的任意两点,
∴△BEF 与△CEF 关于直线 AD 成轴对称.
∴$S_{\triangle CEF}=S_{\triangle BEF}.$
∴$S_{阴影}=S_{\triangle ABE}+S_{\triangle CEF}+S_{\triangle BDF}=S_{\triangle ABE}+S_{\triangle BEF}+S_{\triangle BDF}=S_{\triangle ABD}=6 cm^2.$
∵△ABC是轴对称图形,且直线 AD 是对称轴,
∴△ABD与△ACD关于直线 AD 成轴对称.
∴$S_{\triangle ABD}=S_{\triangle ACD}=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2} × 12=6 (cm^2). $又
∵点 E,F 是 AD 上的任意两点,
∴△BEF 与△CEF 关于直线 AD 成轴对称.
∴$S_{\triangle CEF}=S_{\triangle BEF}.$
∴$S_{阴影}=S_{\triangle ABE}+S_{\triangle CEF}+S_{\triangle BDF}=S_{\triangle ABE}+S_{\triangle BEF}+S_{\triangle BDF}=S_{\triangle ABD}=6 cm^2.$
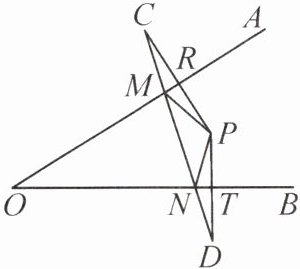
11. 如图,点 P 在∠AOB 内部,点 P 关于 OA,OB 对称的点分别为 C,D,连接 PC 交 OA 于点 R,连接 PD 交 OB 于点 T,连接 CD,交 OA 于点 M,交 OB 于点 N,连接 PM,PN.
(1)若 CD=18 cm,求△PMN 的周长;
(2)若∠C=15°,∠D=17°,求∠MPN 的度数.
(1)若 CD=18 cm,求△PMN 的周长;
(2)若∠C=15°,∠D=17°,求∠MPN 的度数.

答案:
11.解:
∵点 C 和点 P 关于 OA 对称,点 M 在 OA 上,
∴△CMR 与△PMR 关于直线 OA 对称.
∴CM=MP,∠C=∠CPM. 同理可得,DN=PN,∠D=∠DPN.
(1)△PMN 的周长为 PM+MN+PN=CM+MN+DN=CD=18 cm.
(2)在△CDP 中,
∵∠C=15°,∠D=17°,
∴∠CPD=180°-∠C-∠D=180°-15°-17°=148°.
∴∠MPN=∠CPD-∠CPM-∠DPN=∠CPD-∠C-∠D=148°-15°-17°=116°.
∵点 C 和点 P 关于 OA 对称,点 M 在 OA 上,
∴△CMR 与△PMR 关于直线 OA 对称.
∴CM=MP,∠C=∠CPM. 同理可得,DN=PN,∠D=∠DPN.
(1)△PMN 的周长为 PM+MN+PN=CM+MN+DN=CD=18 cm.
(2)在△CDP 中,
∵∠C=15°,∠D=17°,
∴∠CPD=180°-∠C-∠D=180°-15°-17°=148°.
∴∠MPN=∠CPD-∠CPM-∠DPN=∠CPD-∠C-∠D=148°-15°-17°=116°.
查看更多完整答案,请扫码查看


