《2025年高考总复习首选用卷数学人教版》

18.（2023·河南TOP二十名校高三下四月冲刺考（一））已知抛物线$C:y^{2}=2px(p\gt0)$的焦点为$F$，准线为$l$，点$A(3,2\sqrt{3})$在$C$上，直线$AF$与$l$交于点$B$，则$\frac{|AF|}{|BF|}=$（ ）
A. 1
B. $\sqrt{2}$
C. $\sqrt{3}$
D. 2

答案： A　[由A(3,2$\sqrt{3}$)在y²=2px上,有12=2p×3,得p=2,所以F(1,0),|AF|=　$\sqrt{(3−1)²+(2\sqrt{3})²}$=4,过点A作1的垂线，垂足为H,由抛物线的定义可知|AH|=|AF|=4,设l与x轴交于点G,则|FG|=2,有|AH|=2|FG|,又AH//FG,所以F为AB的中点,有|AF|=|BF|,B|AFF|=1.故选A.]

19.（2024·四川巴蜀中学高三适应性月考（二））已知点$F$为抛物线$y^{2}=2\sqrt{3}x$的焦点，过点$F$的直线交抛物线$C$于$A$，$B$两点，$O$为坐标原点，若$\overrightarrow{AF}=3\overrightarrow{FB}$，则$\triangle AOB$的面积为（ ）
A. 3
B. $2\sqrt{3}$
C. $\sqrt{3}$
D. $\frac{\sqrt{3}}{2}$

答案： C[设|FB|=t,则|AF|=3t,如图所示,不妨设AB的倾斜角为锐角0,过A,B分别作抛物线准线的垂线，垂足分别为A,B,则|AA|=3t,|BB|=t,过B作BD⊥AA于点D,则|AD|=2t,
∴COs∠BAD=$\frac{[AD}{AB}$=$\frac{1}{2}$,
∴1的倾斜角0为60°,由结论有SAB=上2si²n=$\frac{3}{3}$=$\sqrt{3}$,当AB的倾斜角为钝角时，一样推导出C成立，故选C.]

20.（多选）（2024·江西红色十校高三联考）已知抛物线$C:y^{2}=2px(p\gt0)$的焦点为$F$，$P(1,m)$为$C$上在第四象限内一点，且$|PF| = 2$，直线$l:y = x + m$与$C$交于$A$，$B$两点，则下列结论正确的是（ ）
A. 抛物线$C$的准线方程为$x = - 1$
B. 点$F$到直线$l$的距离为$\frac{1}{2}$
C. $\triangle AOB$是钝角三角形（$O$为坐标原点）
D. $|AB| = 4\sqrt{6}$

答案： ACD

21.（多选）（2023·江苏苏州模拟）已知$P$为抛物线$C:y^{2}=2px(p\gt0)$上的动点，$Q(4,-4)$在抛物线$C$上，过抛物线$C$的焦点$F$的直线$l$与抛物线$C$交于$A$，$B$两点，$M(3,-2)$，$N(-1,1)$，则（ ）
A. $|PM|+|PF|$的最小值为$4$
B. 若线段$AB$的中点为$M$，则$\triangle NAB$的面积为$\sqrt{2}$
C. 若$NA\perp NB$，则直线$l$的斜率为$2$
D. 过点$E(1,2)$作两条直线与抛物线$C$分别交于$G$，$H$（$G$，$H$不同于点$E$），且满足$EF$平分$\angle GEH$，则直线$GH$的斜率为定值

答案： ACD

22.（2023·福建福州三中校考模拟预测）已知抛物线$y^{2}=4x$与圆$(x - 1)^{2}+y^{2}=1$，过抛物线的焦点$F$作斜率为$k$的直线$l$与抛物线交于$A$，$D$两点，与圆交于$B$，$C$两点（$A$，$B$在$x$轴的同一侧），若$\overrightarrow{AB}=4\overrightarrow{CD}$，则$k^{2}$的值是_______。

答案： 答案　8 解析　抛物线y=4x的焦点F(1,0),于是直线l:y=k(x−1),显然k≠0,由{yy²==k4(xx,−1),消去y,得k²x²−(2k²+4)x+k²=0,设A(x1,y),D(x2,y),则x1+x2=2+$\frac{4}{k²}$,x1x=1,又圆(x−1)²+y²=1的圆心为F(1,0),半径为1,由AB=4CD,得|AB|=4|CD|,即∣AF|−1=4(|DF|−1),于是(x+1)−1=4[(x2+1)−1],整理得x=4x2,又x1x2=1,解得x1=2,x2=$\frac{1}{2}$,则2+$\frac{4}{k²}$=x+x2 =$\frac{5}{2}$,解得k²=8,所以k²的值是8.

23.（2024·河南郑州外国语学校高三上第三次调研考试）已知抛物线$y^{2}=8x$的焦点为$F$，准线与$x$轴的交点为$C$，过点$C$的直线$l$与抛物线交于$A$，$B$两点，若$\angle AFB=\angle CFB$，则$|AF| =$_______。

答案： 答案　8

1.（2023·新课标Ⅰ卷）在直角坐标系$xOy$中，点$P$到$x$轴的距离等于点$P$到点$(0,\frac{1}{2})$的距离，记动点$P$的轨迹为$W$。
（1）求$W$的方程；
（2）已知矩形$ABCD$有三个顶点在$W$上，证明：矩形$ABCD$的周长大于$3\sqrt{3}$。

答案：
解　
(1)设P(x,y),则|y|=　\sqrt{x²+(y−\frac{1}{2}}},两边同时平方，化简得y=x²+$\frac{1}{4}$,故W的方程为y=x²+$\frac{1}{4}$.
(2)证法一:不妨设A,B,D在W上,且AB⊥AD,
　依题意可设A(a,a²+$\frac{1}{4}$),易知直线AB,
　AD的斜率均存在且不为0,
　则设AB,AD的斜率分别为k和一$\frac{1}{k}$,由
　对称性，不妨设|k|≤1,
　直线AB的方程为y=k(x−a)+a²+$\frac{1}{4}$,
　联立
　{y=x²+$\frac{1}{4}$
　y=k(x−a)+a²+$\frac{1}{4}$}
　得x²−kx+ka−a²=0,
　A=k²−4(ka−a²)=(k−2a)²＞0,则k≠2a,
　则|AB|=$\sqrt{1+k²}$1k−2al,
　同理|AD|=/$\sqrt{\frac{1}{k²}}$1+　　|$\frac{1}{k}$+2a|,
　所以|AB|+|AD|=　$\sqrt{1+k²}$1k−2a｜+/$\sqrt{\frac{1}{k²}}$1+　　|$\frac{1}{k}$+2a|
　≥　$\sqrt{1+k²}$(1k−2al+|$\frac{1}{k}$+2a|≥　$\sqrt{1+k²}$|k+$\frac{1}{k}$|
　=　$\sqrt{\frac{(1+k²)}{k²}.}$.
　令k²=m,则m∈(0,1],
　设∮(m)=$\frac{(m+1)3}{m}$=m²+3m+$\frac{1}{m}$+3,
　则f(m)=2m+3−m1²=$\frac{(2m−1)(m+1)²}{m²}$,
　令f(m)=0,解得m=$\frac{1}{2}$,
　当m∈(0.'$\frac{1}{2}$)时,f(m)＜0,f(m)单调递减，
　当m∈($\frac{1}{2}$,1]时,f(m)＞0,f(m))单调递增，,
　则∮((m)m=f($\frac{1}{2}$)=$\frac{27}{4}$,
　所以|AB|+|AD|≥$\frac{3\sqrt{3}}{2}$,
但　$\sqrt{1+k²}$1k−2a|+/1$\sqrt{\frac{1}{k²}}$+　　|$\frac{1}{k}$+2a|≥　$\sqrt{1+k²}$(1k−2a)
+|$\frac{1}{k}$+2a|),此处取等号的条件为||k|=1,与最终取等号的条件|k|=$\frac{√2}{2}$不一致,故|AB∣+|AD|＞32√3,
故矩形ABCD的周长大于3$\sqrt{3}$

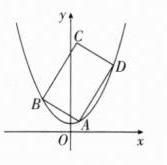
证法二:设矩形的三个顶点A(a,α²+
$\frac{1}{4}$),B(b,b²+$\frac{1}{4}$),c(c,.²+$\frac{1}{4}$
)在W
　上,a所在直线的斜率均存在且不为0,
则kAB.kx=−1,a+b＜b+c,令kAB=
b²+$\frac{1}{4}$−(a²+$\frac{1}{4}$
　　　b−a　　　=a+b=m＜0,
同理,令kx=b+c=n>0,且mn=−1,则m=−$\frac{1}{n}$,
设矩形的周长为l,由对称性,不妨设|m|≥｜Hl,kx−kAB=c一a=n−m=n+$\frac{1}{n}$,
则$\frac{1}{2}$l=|AB|+|BC|=(b−a)　$\sqrt{1+m²}$+(c−b)　$\sqrt{1+n²}$≥(c−aa)$\sqrt{1+n}$=(n+$\frac{1}{n}$)　$\sqrt{1+n}$
n＞0,易知(n+$\frac{1}{n}$)　$\sqrt{1+n²}$＞o,
令f(x)=(x+$\frac{1}{x}$)²(1+x²),x＞0,
f(x)=2(x+$\frac{1}{x}$)²(2x−$\frac{1}{x}$),
令f(x)=0,解得x=$\frac{1}{2}$,
当x∈(0.'$\frac{1}{2}$)时,f(x)＜0,f(x)单调递减,
当x∈($\frac{\sqrt{2}}{2}$,+8{時,f(x)＞0,f(x)单调递增,
则f(x)mm=f($\frac{\sqrt{2}}{2}$)=$\frac{27}{4}$,
故$\frac{1}{2}$$\sqrt{\frac{27}{4}}$=$\frac{3\sqrt{3}}{2}$,即I≥3$\sqrt{3}$
当l=3$\sqrt{3}$时,n=$\frac{1}{2}$,m=−√2,
且(b−a)　$\sqrt{1+m²}$=(b−a)　$\sqrt{1+n²}$,即当|m|=|n|时等号成立,矛盾,故l＞3$\sqrt{3}$,得证

证法三:为了计算方便，我们将抛物线向下移动$\frac{1}{4}$个单位得抛物线W':y=x²,
矩形ABCD变换为矩形A'B{C'D',则问题等价于矩形A'B'C'D’的周长大于3$\sqrt{3}$
设B'(t,²),A'(t,t²),C(2,t2)在W'上,且A'B'⊥B'C',根据对称性，不妨设t。≥0,
则kA.B=t+t,kBc=t2+t,
由于A'B'⊥B'C',则(t1+t0)(t2+t)=−1.
由于|A'B'|=$\sqrt{1+(t+t)²}$1t1−t。1,|B'C'=|　　$\sqrt{1+(t2+t)²}$
1t2−to1,且t介于t,t2之间,不妨设t＜to＜t2,
则|A'B'|+|BC′|=　　$\sqrt{1+(t+t)²}$(;o−t1)+　　$\sqrt{1+(t+t)²}$(t2)
−t0).
令t+1=tanθ,0∈(0,$\frac{π}{2}$),
则t+=−$\frac{1}{tan0}$,
则t=tanθ−to,t1=−$\frac{1}{tan0}$−to,
　所以|A'B'|+|B'C'|=/$\sqrt{\frac{1}{tan²0}}$1+　　(2to+$\frac{1}{tano}$)+　$\sqrt{1+tan0}$.(tanθ−2t),
　故|A'B'|+|B'C'|=2to($\frac{1}{sin0}$"$\frac{1}{cos0}$+$\frac{sino}{cos²0}$+$\frac{cos0}{sin0}$=
　$\frac{2t(cos0−sinθ)}{sin0cos0}$+$\frac{sin²0+cos²0}{sin²0cos²0}$
　①当θ∈(0,$\frac{π}{4}$]時,
　|A'B'|+|B'C'|≥$\frac{sin²0+cos²0}{sin²0cos²0}$=$\frac{sino}{cos²0}$+$\frac{cos0}{sin0}$≥2　$\sqrt{\frac{1}{sin0cos0}}$=
　2　$\sqrt{\frac{2}{sin20}}$≥2＞322;
　②当0E($\frac{π}{4}$,$\frac{π}{2}$)时,由于1＜t＜t2,
　从而一$\frac{1}{tan0}$−t＜t。＜tanθ−to,
　从而一$\frac{1}{2tan0}$＜t＜$\frac{tano}{2}$,
　又t≥0,
　故0≤t。＜$\frac{tan0}{2}$,
　所以|A'B'|+|B'C'|=$\frac{2t。(cosθ−sinθ)}{sinfcos0}$+$\frac{sin0+cos²0}{sin²0cos²0}$
　＞$\frac{sinθ(cosθ−sin0)}{sinocos²0}$+$\frac{sin0+cos²0}{sin²0cos²0}$=$\frac{1}{sin²0cosf}$$\sqrt{sini.2}$
　≥　$\sqrt{[\frac{(1−cos²θ)+(1−cos²0)+2cos²0}{3}23}$
　=　　　　=$\frac{3√3}{2}$,
　当且仅当cos0=$\frac{\sqrt{3}}{3}$时等号成立,故|A'B'|
　+|B'C'|＞$\frac{3√3}{2}$,故矩形ABCD的周长大于3$\sqrt{3}$